Question

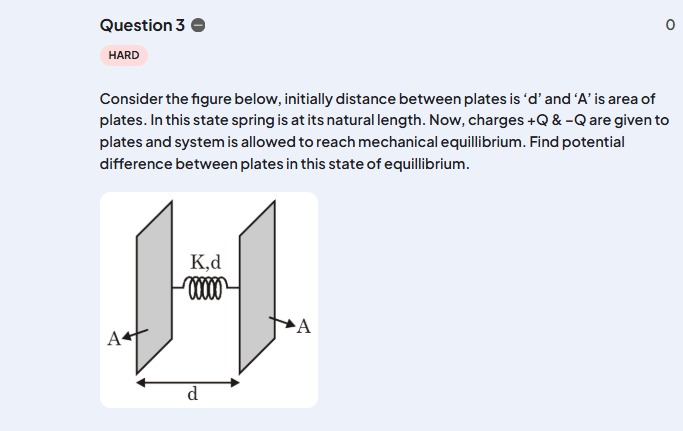
Consider the figure below, initially distance between plates is 'd' and 'A' is area of plates. In this state spring is at its natural length. Now, charges +Q & -Q are given to plates and system is allowed to reach mechanical equillibrium. Find potential difference between plates in this state of equillibrium.

Answer 1

$V = \frac{Qd}{\epsilon_0 A} - \frac{Q^3}{2K\epsilon_0^2 A^2}$

Answer 2

1. Forces at Equilibrium: In the equilibrium state, the attractive electrostatic force between the charged plates must be balanced by the repulsive force exerted by the compressed spring.

   • The electrostatic force between two parallel plates with charge $Q$ and area $A$ separated by a distance $d'$ is $F_e = \frac{Q^2}{2\epsilon_0 A}$. This force is attractive.
   • Initially, the distance between the plates is $d$, and the spring is at its natural length. When the plates move closer to $d'$, the spring is compressed by $(d - d')$. The spring force is $F_s = K(d - d')$, which is repulsive.
   • At equilibrium, $F_e = F_s$, so $\frac{Q^2}{2\epsilon_0 A} = K(d - d')$.

2. Equilibrium Separation: From the equilibrium equation, we can find the new separation $d'$: $d - d' = \frac{Q^2}{2K\epsilon_0 A}$ $d' = d - \frac{Q^2}{2K\epsilon_0 A}$

3. Potential Difference: The potential difference $V$ between the plates of a parallel plate capacitor is given by $V = \frac{Q}{C}$, where $C = \frac{\epsilon_0 A}{d'}$ is the capacitance at separation $d'$. Therefore, $V = \frac{Q}{(\epsilon_0 A / d')} = \frac{Q d'}{\epsilon_0 A}$.

4. Substitute Equilibrium Separation: Substitute the expression for $d'$ into the equation for $V$: $V = \frac{Q}{\epsilon_0 A} \left( d - \frac{Q^2}{2K\epsilon_0 A} \right)$ $V = \frac{Qd}{\epsilon_0 A} - \frac{Q^3}{2K\epsilon_0^2 A^2}$