Question: If $\int \frac{dx}{x^{2025}+x} = \frac{1}{a}ln(\frac{x^b}{1+x^c})+C$, where $a, b, c \in N$ and need...

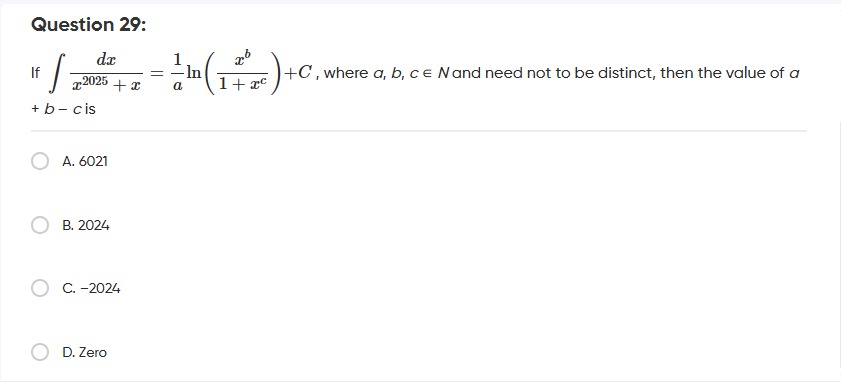
Question

If $\int \frac{dx}{x^{2025}+x} = \frac{1}{a}ln(\frac{x^b}{1+x^c})+C$ , where $a, b, c \in N$ and need not to be distinct, then the value of $a+b-c$ is

Answer 1

Solution

The integral is $\int \frac{dx}{x^{2025}+x}$ . We rewrite the integrand as $\frac{1}{x(x^{2024}+1)}$ . Let $u = x^{2024}$ . Then $du = 2024x^{2023}dx$ . Rewrite the integral as $\int \frac{x^{2023}dx}{x^{2024}(x^{2024}+1)} = \frac{1}{2024} \int \frac{du}{u(u+1)}$ . Using partial fractions, $\frac{1}{u(u+1)} = \frac{1}{u} - \frac{1}{u+1}$ . The integral becomes $\frac{1}{2024} \int (\frac{1}{u} - \frac{1}{u+1})du = \frac{1}{2024} (\ln|u| - \ln|u+1|) + C = \frac{1}{2024} \ln|\frac{u}{u+1}| + C$ . Substituting back $u=x^{2024}$ , we get $\frac{1}{2024} \ln(\frac{x^{2024}}{x^{2024}+1}) + C$ . Comparing with $\frac{1}{a}ln(\frac{x^b}{1+x^c})+C$ , we have $a=2024, b=2024, c=2024$ . Therefore, $a+b-c = 2024+2024-2024 = 2024$ .