Question
Question: The charge on each of the capacitors 0.16 ms after the switch S is closed in figure is : ...
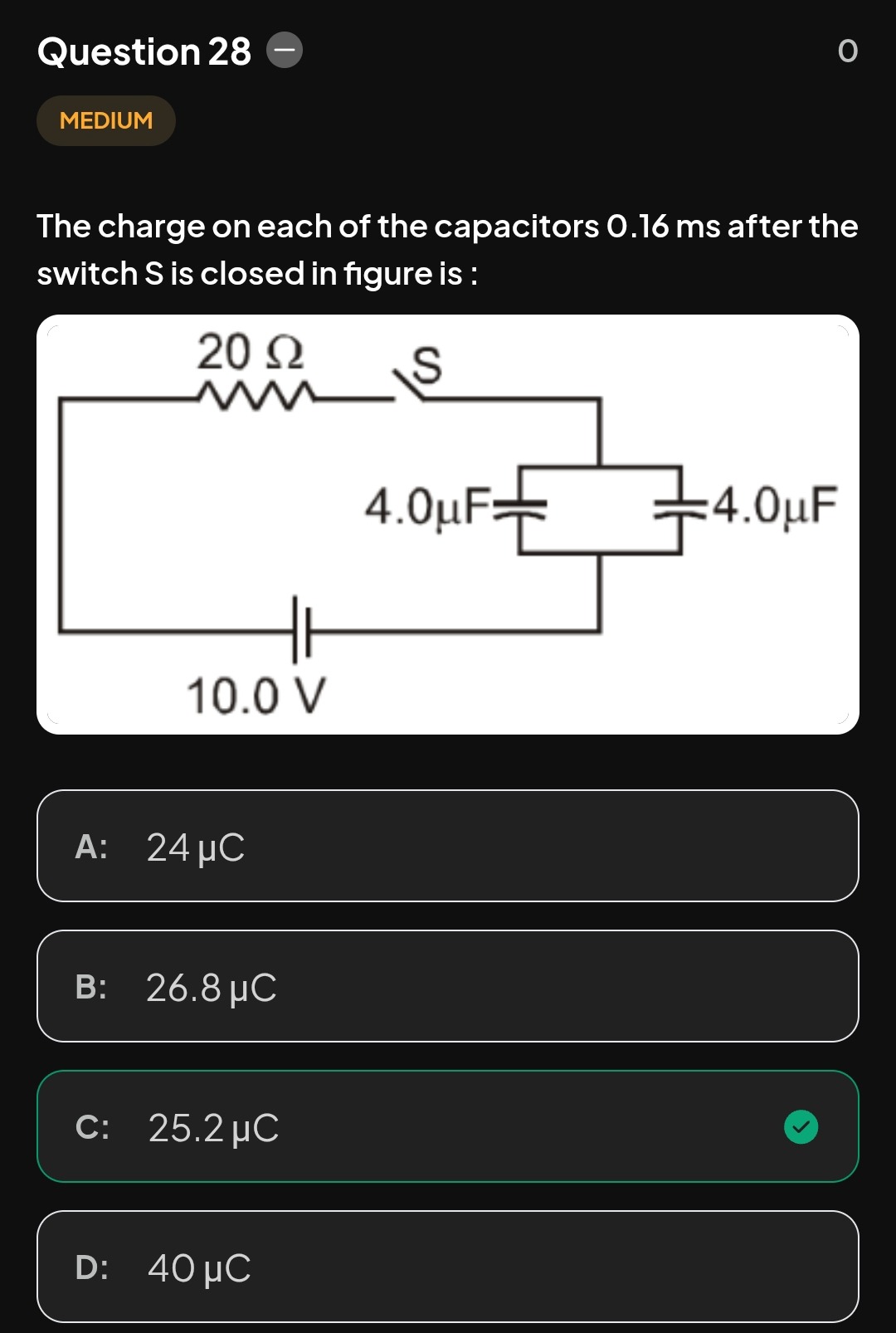
The charge on each of the capacitors 0.16 ms after the switch S is closed in figure is :
24 μC
26.8 μC
25.2 μC
40 μC
25.2 μC
Solution
To find the charge on each capacitor after 0.16 ms, we follow these steps:
-
Calculate Equivalent Capacitance (Ceq): The two capacitors, C1=4.0μF and C2=4.0μF, are connected in parallel. Ceq=C1+C2=4.0μF+4.0μF=8.0μF=8.0×10−6F
-
Calculate Maximum Charge (Qmax): The maximum charge stored on the equivalent capacitor is: Qmax=Ceq×V=(8.0×10−6F)×(10.0V)=80×10−6C=80μC
-
Calculate Time Constant (τ): The time constant for an RC circuit is given by: τ=R×Ceq Given Resistance R=20Ω. τ=(20Ω)×(8.0×10−6F)=160×10−6s=0.16×10−3s=0.16ms
-
Calculate Charge on Equivalent Capacitor at time t: Q(t)=Qmax(1−e−t/τ) Given time t=0.16ms. Since t=τ=0.16ms, the ratio t/τ=1. Q(t)=80μC(1−e−1) Using the value e−1≈0.36788: Q(t)=80μC(1−0.36788) Q(t)=80μC(0.63212) Q(t)=50.5696μC
-
Calculate Charge on Each Capacitor: Charge on each capacitor = 2Q(t)=250.5696μC=25.2848μC≈25.3μC
Therefore, the charge on each capacitor is approximately 25.3μC, which is closest to option C: 25.2μC.
