Question

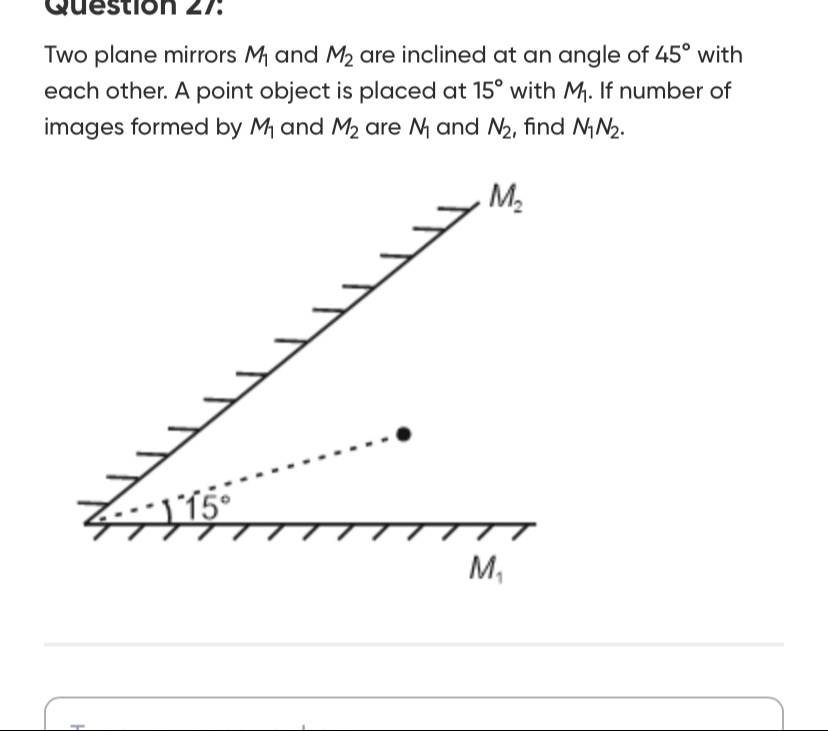
Two plane mirrors $M_1$ and $M_2$ are inclined at an angle of $45^\circ$ with each other. A point object is placed at $15^\circ$ with $M_1$. If number of images formed by $M_1$ and $M_2$ are $N_1$ and $N_2$, find $N_1N_2$.

Answer 1

49

Answer 2

The number of images ($N$) formed by two plane mirrors inclined at an angle $\theta$ is given by:

$n = \frac{360^\circ}{\theta}$

Case 1: If $n$ is an even integer, the number of images formed is $N = n - 1$.

In this problem, $\theta = 45^\circ$. $n = \frac{360^\circ}{45^\circ} = 8$

Since $n=8$ is an even integer, the total number of distinct images formed is: $N = n - 1 = 8 - 1 = 7$.

$N_1 = N = 7$ $N_2 = N = 7$

Then, $N_1N_2 = 7 \times 7 = 49$.