Question

Two converging lenses of focal length 20 cm and 30 cm are placed at a seperation d cm as shown. An object is kept at a distance x from first lens as shown. If the height of image is independent of x, find d.

Answer 1

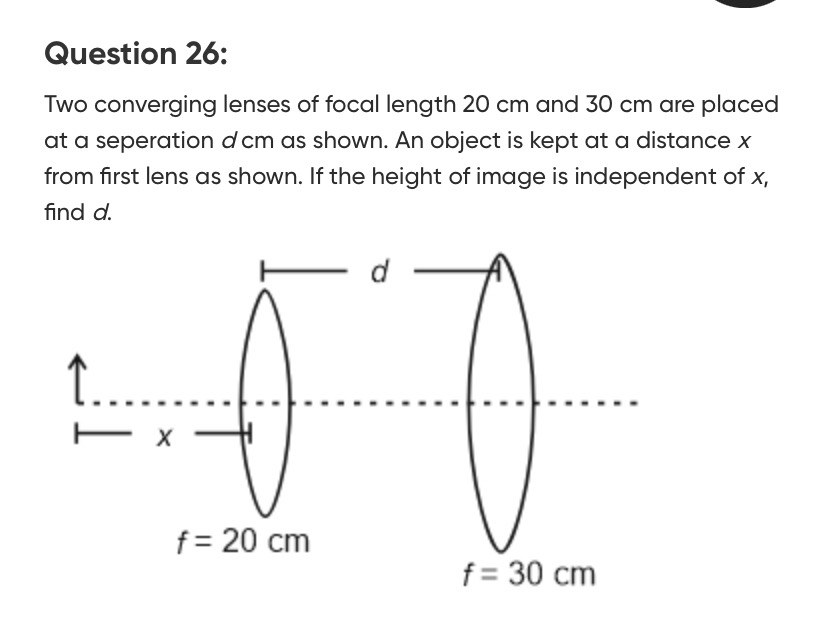
50 cm

Answer 2

The problem requires the final image height to be independent of the object distance 'x'. This implies that the overall magnification of the two-lens system must be constant. We derive the total magnification by considering image formation by the first lens, and then using that image as the object for the second lens. The total magnification $M$ is found to be $M = \frac{-600}{(50 - d)x + (20d - 600)}$. For $M$ to be independent of $x$, the coefficient of $x$ in the denominator must be zero, i.e., $50 - d = 0$. This yields $d = 50$ cm. This condition corresponds to an afocal (telescopic) system, where the separation between the lenses is the sum of their focal lengths ($d = f_1 + f_2$).