Question

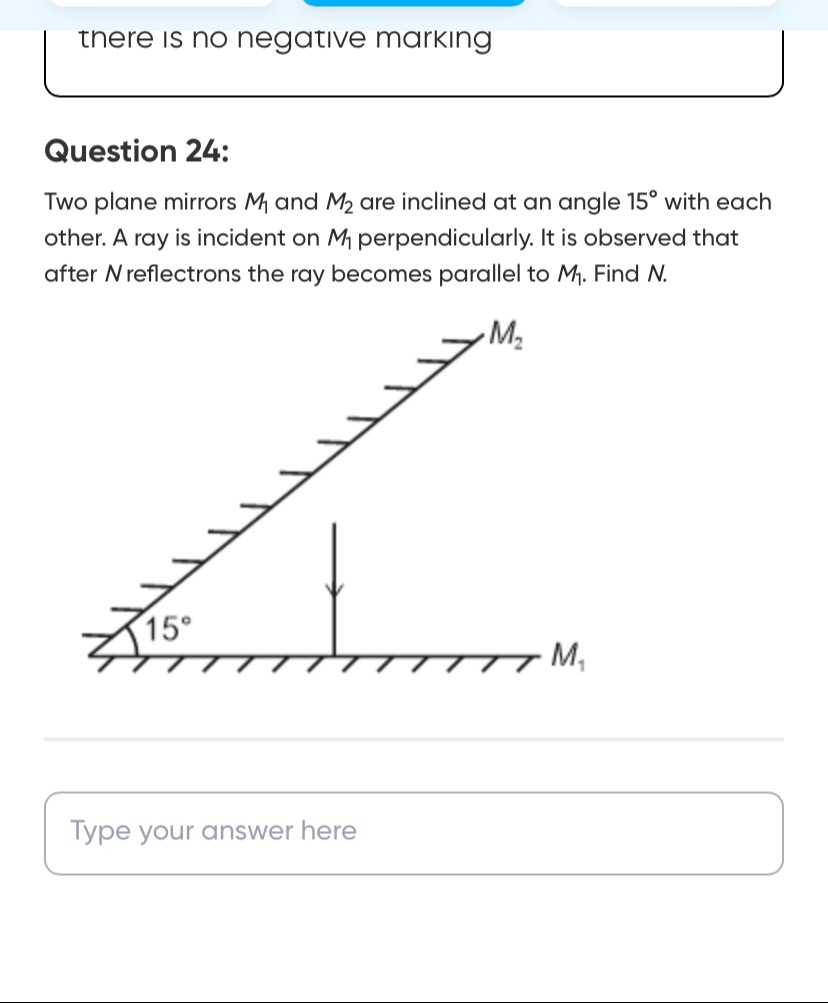
Two plane mirrors $M_1$ and $M_2$ are inclined at an angle $15^\circ$ with each other. A ray is incident on $M_1$ perpendicularly. It is observed that after $N$ reflectrons the ray becomes parallel to $M_1$. Find $N$.

• A. 3
• B. 4
• C. 5
• D. 6

Answer 1

Answer: (D)

6

Answer 2

Let $\alpha_k$ be the angle of the ray with $M_1$ after $k$ reflections.

• Initial ray is perpendicular to $M_1$. So, $\alpha_0 = 90^\circ$.

• 1st reflection (on $M_1$): The ray is reflected. $\alpha_1 = 90^\circ$.

• This ray hits $M_2$. The angle of incidence (with normal to $M_2$) is $i_2 = 90^\circ - (90^\circ - \theta) = \theta = 15^\circ$.

• 2nd reflection (on $M_2$): The ray reflects from $M_2$. The angle of the reflected ray with $M_2$ is $90^\circ - i_2 = 90^\circ - 15^\circ = 75^\circ$.

• The angle of this ray with $M_1$: The ray is at $75^\circ$ to $M_2$. $M_2$ is at $15^\circ$ to $M_1$.

• So, the angle of the ray with $M_1$ is $75^\circ - 15^\circ = 60^\circ$ (if it is between $M_1$ and $M_2$). So, $\alpha_2 = 60^\circ$.

• 3rd reflection (on $M_1$): The ray hits $M_1$ at $60^\circ$. So, $i_3 = 90^\circ - 60^\circ = 30^\circ$.

• The reflected ray from $M_1$ makes $60^\circ$ with $M_1$. So $\alpha_3 = 60^\circ$.

• This ray hits $M_2$. The angle it makes with $M_2$ is $60^\circ - 15^\circ = 45^\circ$.

• The angle of incidence on $M_2$ is $i_4 = 90^\circ - 45^\circ = 45^\circ$.

• 4th reflection (on $M_2$): The ray reflects from $M_2$ at $45^\circ$ from its normal.

• The angle of the reflected ray with $M_2$ is $45^\circ$.

• The angle of this ray with $M_1$ is $45^\circ - 15^\circ = 30^\circ$. So $\alpha_4 = 30^\circ$.

• 5th reflection (on $M_1$): The ray hits $M_1$ at $30^\circ$. So $i_5 = 90^\circ - 30^\circ = 60^\circ$.

• The reflected ray from $M_1$ makes $30^\circ$ with $M_1$. So $\alpha_5 = 30^\circ$.

• This ray hits $M_2$. The angle it makes with $M_2$ is $30^\circ - 15^\circ = 15^\circ$.

• The angle of incidence on $M_2$ is $i_6 = 90^\circ - 15^\circ = 75^\circ$.

• 6th reflection (on $M_2$): The ray reflects from $M_2$ at $75^\circ$ from its normal.

• The angle of the reflected ray with $M_2$ is $15^\circ$.

• The angle of this ray with $M_1$ is $15^\circ - 15^\circ = 0^\circ$. So $\alpha_6 = 0^\circ$.

When the angle of the ray with $M_1$ becomes $0^\circ$, it means the ray is parallel to $M_1$. This happened after 6 reflections.