Question

A capacitor has a capacity C and reactance X, if capacitance and frequency become triple then reactance will be:

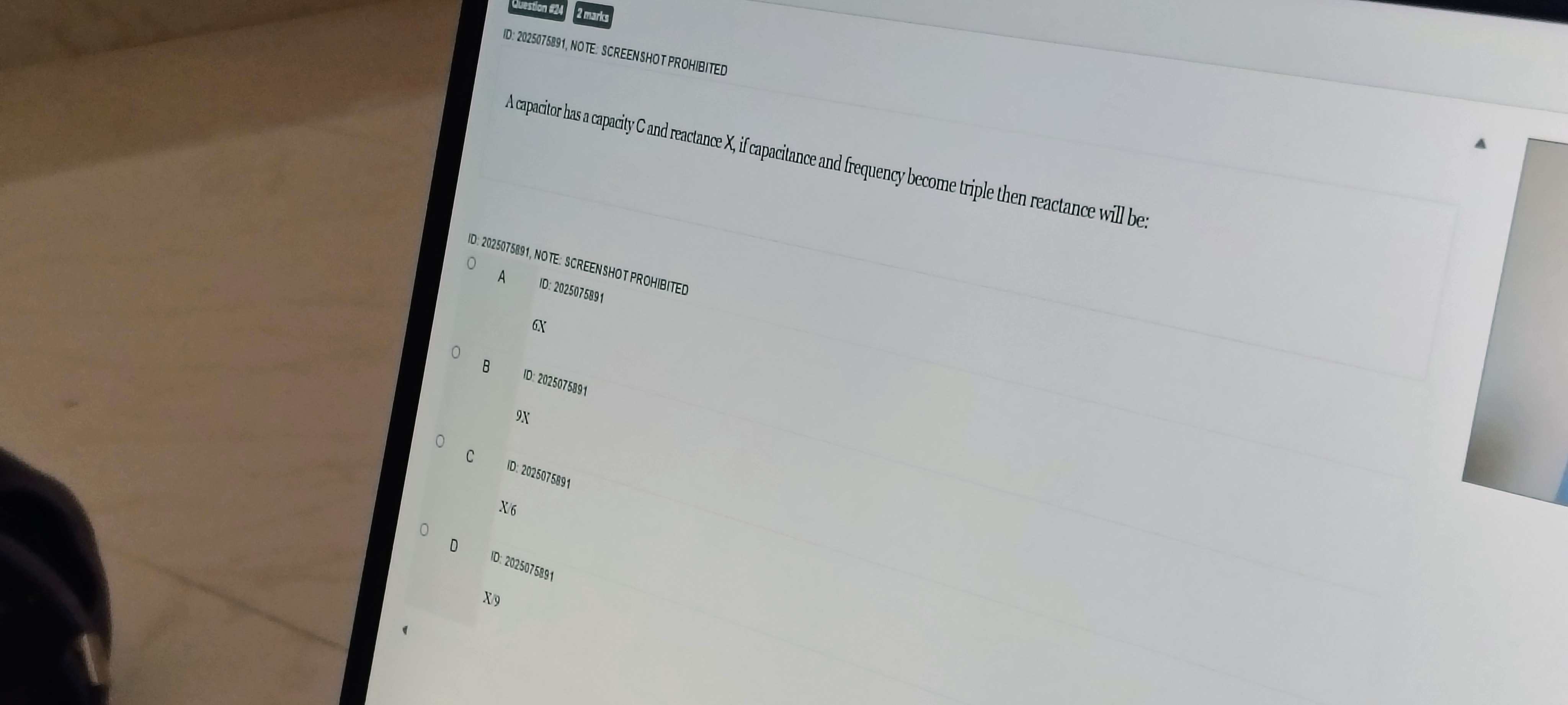
• A. 6X
• B. 9X
• C. X/6
• D. X/9

Answer 1

Answer: (D)

X/9

Answer 2

The capacitive reactance ($X$) is inversely proportional to both the capacitance ($C$) and the frequency ($f$). The formula for capacitive reactance is given by:

$X = \frac{1}{\omega C}$

where $\omega$ is the angular frequency. Since $\omega = 2\pi f$, the formula can also be written as:

$X = \frac{1}{2\pi f C}$

Let the initial capacitance be $C_{initial} = C$ and the initial frequency be $f_{initial} = f$. The initial reactance is $X_{initial} = X = \frac{1}{2\pi f C}$.

According to the problem, the capacitance becomes triple and the frequency also becomes triple. So, the new capacitance is $C_{new} = 3C$. And the new frequency is $f_{new} = 3f$.

Now, let's calculate the new reactance, $X_{new}$:

$X_{new} = \frac{1}{2\pi f_{new} C_{new}}$

Substitute the new values of frequency and capacitance:

$X_{new} = \frac{1}{2\pi (3f) (3C)}$

$X_{new} = \frac{1}{2\pi (9fC)}$

$X_{new} = \frac{1}{9} \left(\frac{1}{2\pi f C}\right)$

We know that $X = \frac{1}{2\pi f C}$. Therefore, we can substitute $X$ into the equation for $X_{new}$:

$X_{new} = \frac{1}{9} X$

$X_{new} = \frac{X}{9}$

Thus, if both the capacitance and frequency become triple, the reactance will become one-ninth of its original value.