Solveeit Logo
Login

Question

Question: $\lim_{x \to -1^+} \frac{\sqrt{x}-\sqrt{\cos^{-1}x}}{\sqrt{x+1}}=$...

lim⁡x→−1+x−cos⁡−1xx+1=\lim_{x \to -1^+} \frac{\sqrt{x}-\sqrt{\cos^{-1}x}}{\sqrt{x+1}}=

Answer

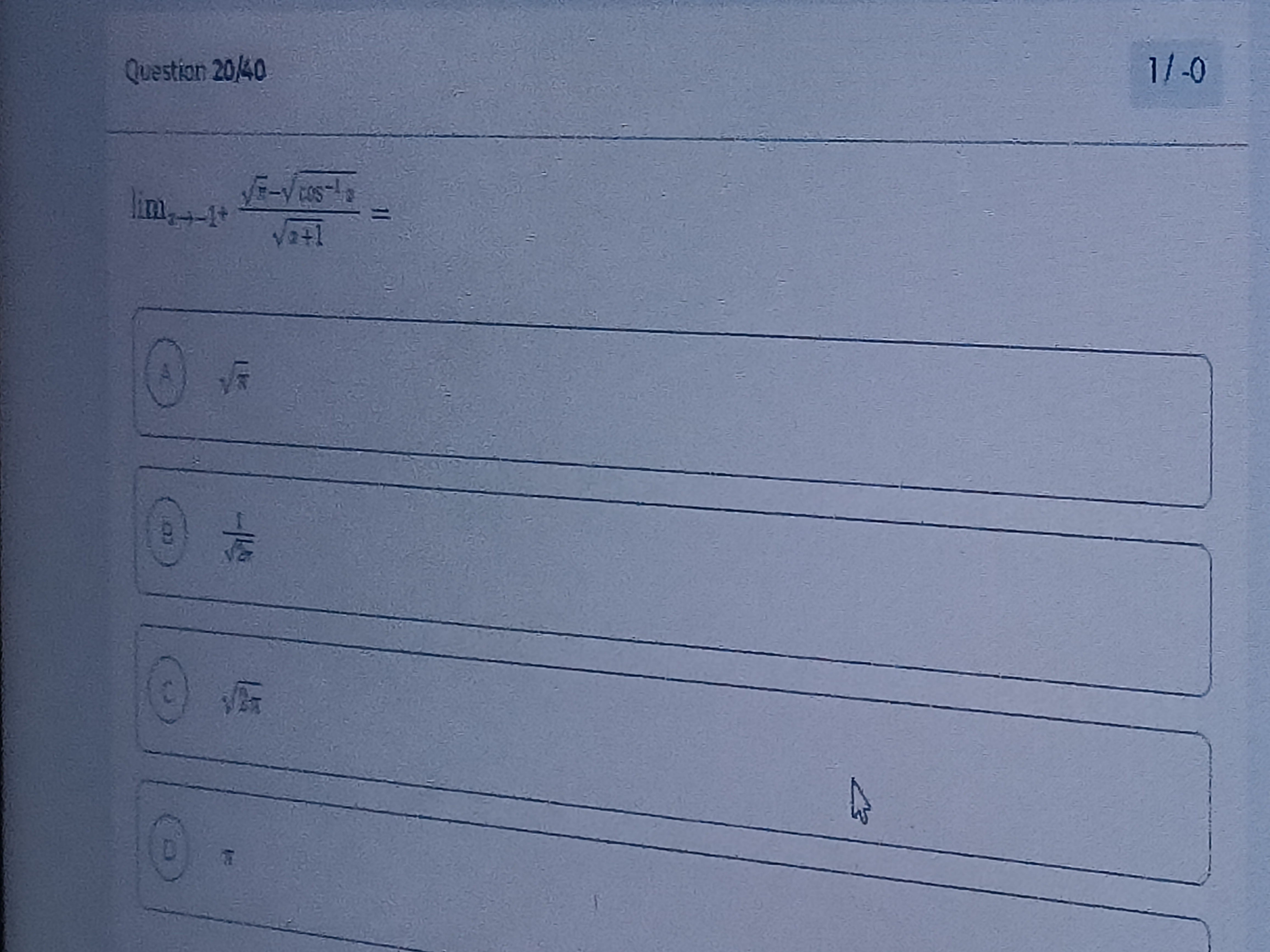
1/sqrt(2*pi)

Explanation

Solution

The given limit is lim⁡x→−1+x−cos⁡−1xx+1\lim_{x \to -1^+} \frac{\sqrt{x}-\sqrt{\cos^{-1}x}}{\sqrt{x+1}}.

First, let's analyze the domain of the functions involved:

  1. x\sqrt{x}: Requires x≥0x \ge 0.
  2. x+1\sqrt{x+1}: Requires x+1≥0⇒x≥−1x+1 \ge 0 \Rightarrow x \ge -1.
  3. cos⁡−1x\cos^{-1}x: Requires −1≤x≤1-1 \le x \le 1.
  4. cos⁡−1x\sqrt{\cos^{-1}x}: Requires cos⁡−1x≥0\cos^{-1}x \ge 0. The range of cos⁡−1x\cos^{-1}x is [0,π][0, \pi], so this is always satisfied when cos⁡−1x\cos^{-1}x is defined.

The limit is taken as x→−1+x \to -1^+. This means xx approaches −1-1 from values greater than −1-1 (e.g., x=−0.99x = -0.99). For such values of xx, the term x\sqrt{x} is not defined in the real number system (e.g., −0.99\sqrt{-0.99} is an imaginary number). Since the options are real numbers, and typically in JEE/NEET, functions are considered over real numbers unless specified, this indicates a potential typo in the question.

Assuming there is a typo and the first term in the numerator was intended to be π\sqrt{\pi} (the value of cos⁡−1(−1)\cos^{-1}(-1)), the limit expression becomes: lim⁡x→−1+π−cos⁡−1xx+1\lim_{x \to -1^+} \frac{\sqrt{\pi}-\sqrt{\cos^{-1}x}}{\sqrt{x+1}}

Now, let's evaluate this limit: As x→−1+x \to -1^+: Numerator: π−cos⁡−1(−1)=π−π=0\sqrt{\pi}-\sqrt{\cos^{-1}(-1)} = \sqrt{\pi}-\sqrt{\pi} = 0. Denominator: −1+1=0=0\sqrt{-1+1} = \sqrt{0} = 0. This is an indeterminate form of type 00\frac{0}{0}, so we can use L'Hopital's rule or series expansion.

Method 1: Using L'Hopital's Rule Let f(x)=π−cos⁡−1xf(x) = \sqrt{\pi}-\sqrt{\cos^{-1}x} and g(x)=x+1g(x) = \sqrt{x+1}. f′(x)=ddx(π−cos⁡−1x)=0−12cos⁡−1x⋅ddx(cos⁡−1x)f'(x) = \frac{d}{dx}(\sqrt{\pi}-\sqrt{\cos^{-1}x}) = 0 - \frac{1}{2\sqrt{\cos^{-1}x}} \cdot \frac{d}{dx}(\cos^{-1}x) f′(x)=−12cos⁡−1x⋅−11−x2=12cos⁡−1x1−x2f'(x) = - \frac{1}{2\sqrt{\cos^{-1}x}} \cdot \frac{-1}{\sqrt{1-x^2}} = \frac{1}{2\sqrt{\cos^{-1}x}\sqrt{1-x^2}}. g′(x)=ddx(x+1)=12x+1g'(x) = \frac{d}{dx}(\sqrt{x+1}) = \frac{1}{2\sqrt{x+1}}.

Applying L'Hopital's Rule: lim⁡x→−1+f′(x)g′(x)=lim⁡x→−1+12cos⁡−1x1−x212x+1\lim_{x \to -1^+} \frac{f'(x)}{g'(x)} = \lim_{x \to -1^+} \frac{\frac{1}{2\sqrt{\cos^{-1}x}\sqrt{1-x^2}}}{\frac{1}{2\sqrt{x+1}}} =lim⁡x→−1+x+1cos⁡−1x1−x2= \lim_{x \to -1^+} \frac{\sqrt{x+1}}{\sqrt{\cos^{-1}x}\sqrt{1-x^2}} We know that 1−x2=(1−x)(1+x)=1−x1+x\sqrt{1-x^2} = \sqrt{(1-x)(1+x)} = \sqrt{1-x}\sqrt{1+x} (since x→−1+x \to -1^+, 1+x>01+x > 0). So the expression becomes: =lim⁡x→−1+x+1cos⁡−1x1−xx+1= \lim_{x \to -1^+} \frac{\sqrt{x+1}}{\sqrt{\cos^{-1}x}\sqrt{1-x}\sqrt{x+1}} =lim⁡x→−1+1cos⁡−1x1−x= \lim_{x \to -1^+} \frac{1}{\sqrt{\cos^{-1}x}\sqrt{1-x}}

Now, substitute x=−1x = -1: =1cos⁡−1(−1)1−(−1)= \frac{1}{\sqrt{\cos^{-1}(-1)}\sqrt{1-(-1)}} =1π2= \frac{1}{\sqrt{\pi}\sqrt{2}} =12π= \frac{1}{\sqrt{2\pi}}

Method 2: Using Substitution and Series Expansion Let x=−1+hx = -1 + h, where h→0+h \to 0^+. The limit becomes lim⁡h→0+π−cos⁡−1(−1+h)h\lim_{h \to 0^+} \frac{\sqrt{\pi}-\sqrt{\cos^{-1}(-1+h)}}{\sqrt{h}}. Let y=cos⁡−1(−1+h)y = \cos^{-1}(-1+h). As h→0+h \to 0^+, y→cos⁡−1(−1)=πy \to \cos^{-1}(-1) = \pi. Let y=π−θy = \pi - \theta, where θ→0+\theta \to 0^+. Then cos⁡y=cos⁡(π−θ)=−cos⁡θ\cos y = \cos(\pi - \theta) = -\cos\theta. So, −1+h=−cos⁡θ-1+h = -\cos\theta. cos⁡θ=1−h\cos\theta = 1-h. For small θ\theta, we use the Taylor expansion cos⁡θ≈1−θ22\cos\theta \approx 1 - \frac{\theta^2}{2}. So 1−θ22≈1−h⇒θ22≈h⇒θ≈2h1 - \frac{\theta^2}{2} \approx 1-h \Rightarrow \frac{\theta^2}{2} \approx h \Rightarrow \theta \approx \sqrt{2h} (since θ>0\theta > 0).

Substitute this back into the limit expression: lim⁡h→0+π−π−θh\lim_{h \to 0^+} \frac{\sqrt{\pi}-\sqrt{\pi-\theta}}{\sqrt{h}} Substitute θ=2h\theta = \sqrt{2h}: =lim⁡h→0+π−π−2hh= \lim_{h \to 0^+} \frac{\sqrt{\pi}-\sqrt{\pi-\sqrt{2h}}}{\sqrt{h}} Multiply the numerator and denominator by the conjugate of the numerator: =lim⁡h→0+(π)2−(π−2h)2h(π+π−2h)= \lim_{h \to 0^+} \frac{(\sqrt{\pi})^2-(\sqrt{\pi-\sqrt{2h}})^2}{\sqrt{h}(\sqrt{\pi}+\sqrt{\pi-\sqrt{2h}})} =lim⁡h→0+π−(π−2h)h(π+π−2h)= \lim_{h \to 0^+} \frac{\pi-(\pi-\sqrt{2h})}{\sqrt{h}(\sqrt{\pi}+\sqrt{\pi-\sqrt{2h}})} =lim⁡h→0+2hh(π+π−2h)= \lim_{h \to 0^+} \frac{\sqrt{2h}}{\sqrt{h}(\sqrt{\pi}+\sqrt{\pi-\sqrt{2h}})} =lim⁡h→0+2hh(π+π−2h)= \lim_{h \to 0^+} \frac{\sqrt{2}\sqrt{h}}{\sqrt{h}(\sqrt{\pi}+\sqrt{\pi-\sqrt{2h}})} =lim⁡h→0+2π+π−2h= \lim_{h \to 0^+} \frac{\sqrt{2}}{\sqrt{\pi}+\sqrt{\pi-\sqrt{2h}}} Now, substitute h=0h=0: =2π+π−0=2π+π=22π= \frac{\sqrt{2}}{\sqrt{\pi}+\sqrt{\pi-0}} = \frac{\sqrt{2}}{\sqrt{\pi}+\sqrt{\pi}} = \frac{\sqrt{2}}{2\sqrt{\pi}} =12π=12π= \frac{1}{\sqrt{2}\sqrt{\pi}} = \frac{1}{\sqrt{2\pi}}

Both methods yield the same result, which matches option B.

The final answer is 12π\boxed{\frac{1}{\sqrt{2\pi}}}.