Question

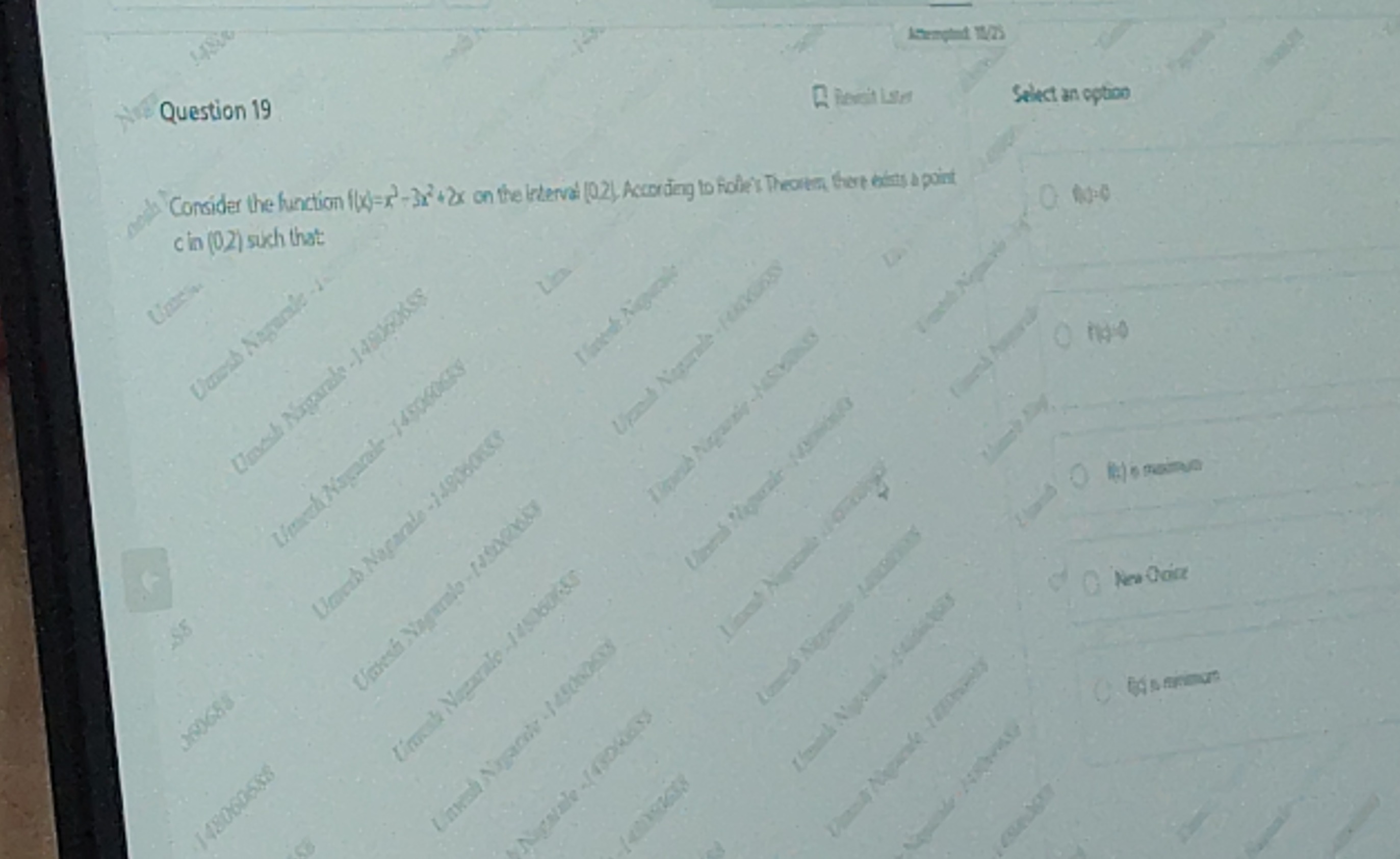
Consider the function $f(x) = x^3 - 3x^2 + 2x$ on the interval (0,2). According to Rolle's Theorem, there exists a point c in (0,2) such that:

• A. f(c)=0
• B. f'(c)=0
• C. f(c) is maximum
• D. New Choice
• E. f(c) is minimum

Answer 1

Answer: (B)

f'(c)=0

Answer 2

Rolle's Theorem states that if a function is continuous on a closed interval, differentiable on the open interval, and has equal values at the endpoints, then there exists at least one point within the open interval where its derivative is zero. All conditions are met for the given function and interval: $f(x)$ is a polynomial (hence continuous and differentiable everywhere), and $f(0) = 0$ and $f(2) = 0$, so $f(0) = f(2)$. Therefore, by Rolle's Theorem, there exists a $c \in (0,2)$ such that $f'(c) = 0$.