Question
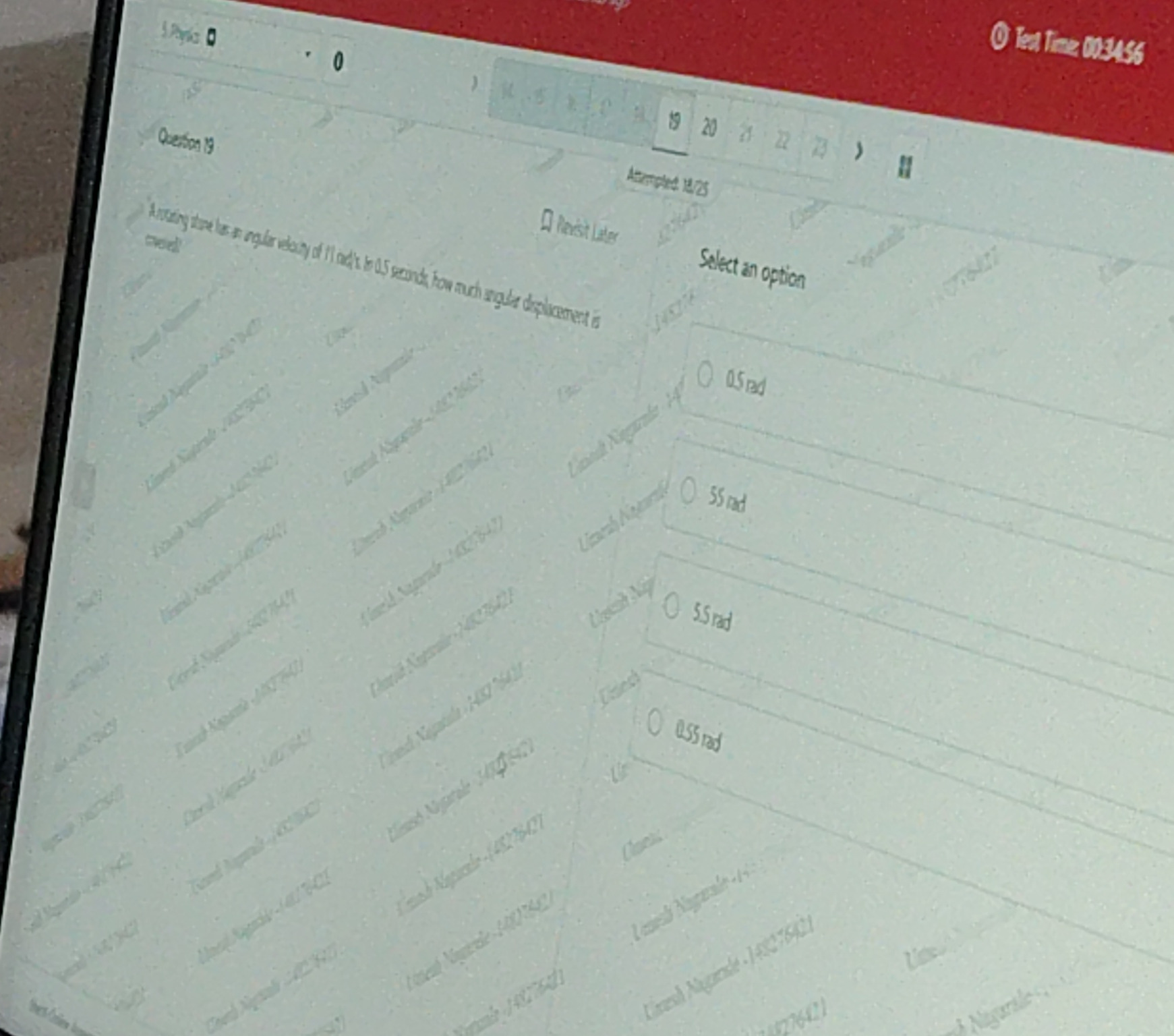
Question: A rotating stone has an angular velocity of 11 rad/s. In 0.5 seconds, how much angular displacement ...
A rotating stone has an angular velocity of 11 rad/s. In 0.5 seconds, how much angular displacement is overall?
A
0.5 rad
B
5.5 rad
C
0.55 rad
Answer
5.5 rad
Explanation
Solution
The problem asks for the angular displacement of a rotating stone given its angular velocity and the time duration. Assuming the angular velocity is constant, the angular displacement (Δθ) can be calculated using the formula:
Δθ=ω×t
where ω is the angular velocity and t is the time.
Given values: Angular velocity (ω) = 11 rad/s Time (t) = 0.5 s
Substitute these values into the formula:
Δθ=(11 rad/s)×(0.5 s) Δθ=5.5 rad
Thus, the overall angular displacement is 5.5 radians.
