Question
Question: $\int \frac{sin x}{3+4cos^2x}dx = Atan^{-1}(Bcosx)+c$ where c is a constant of integration. Then, t...
∫3+4cos2xsinxdx=Atan−1(Bcosx)+c
where c is a constant of integration. Then, the value of A+B is:
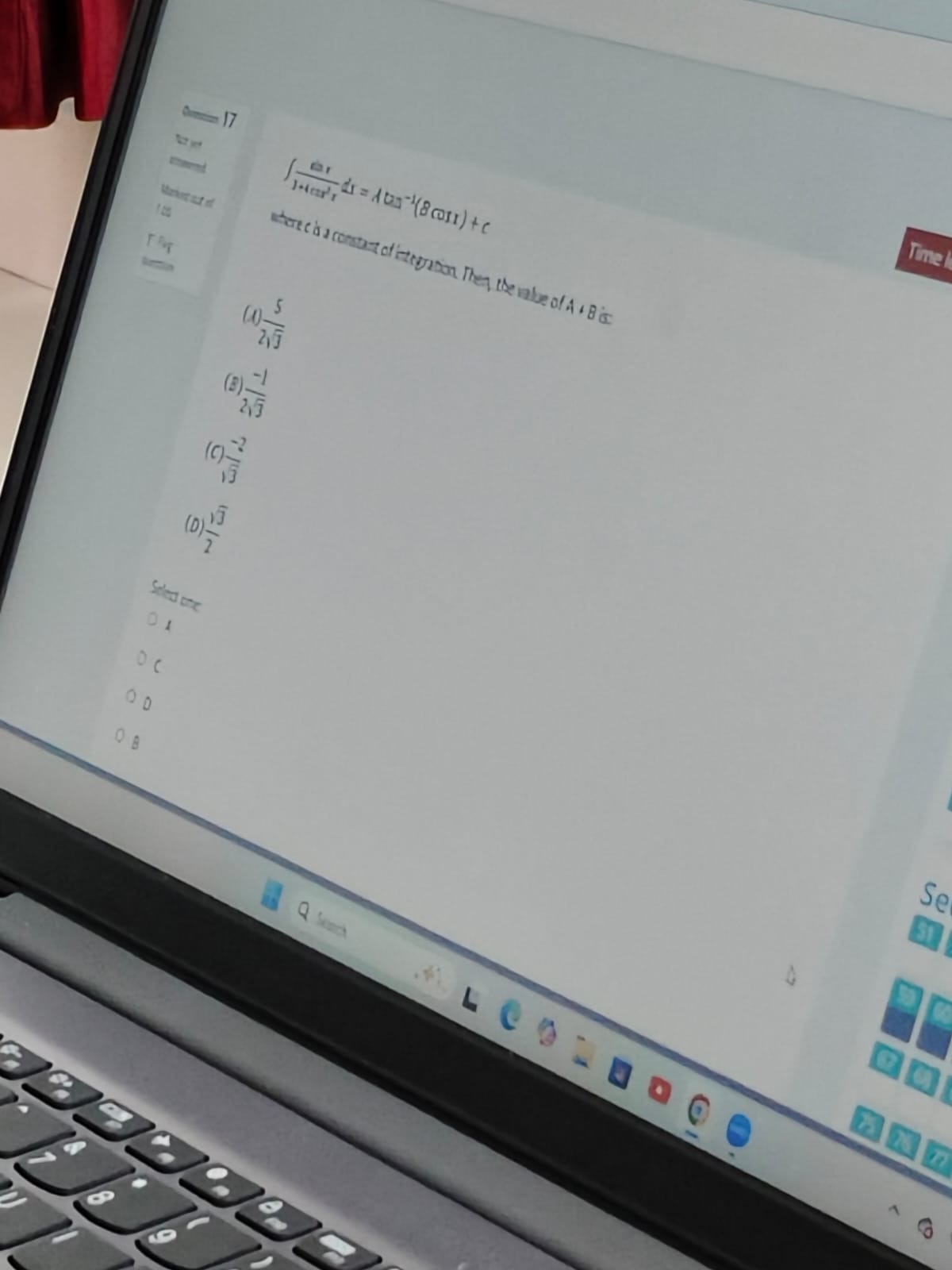
235
23−1
3−2
23
23
Solution
To evaluate the integral ∫3+4cos2xsinxdx, we use the method of substitution.
Let u=cosx. Differentiating both sides with respect to x, we get: du=−sinxdx This implies sinxdx=−du.
Substitute these into the integral: ∫3+4cos2xsinxdx=∫3+4u2−du =−∫4u2+3du Factor out 4 from the denominator: =−41∫u2+43du This integral is of the standard form ∫x2+a2dx=a1tan−1(ax)+C. In our case, x=u and a2=43, so a=43=23.
Applying the formula: −41[231tan−1(23u)]+c =−41[32tan−1(32u)]+c =−231tan−1(32u)+c Now, substitute back u=cosx: =−231tan−1(32cosx)+c
The given form of the integral is Atan−1(Bcosx)+c. Comparing our result with the given form: A=−231 B=32
We need to find the value of A+B: A+B=−231+32 To add these fractions, we find a common denominator, which is 23: A+B=−231+232×2 A+B=−231+234 A+B=23−1+4 A+B=233 To simplify, we can rationalize the denominator by multiplying the numerator and denominator by 3: A+B=233×33 A+B=2×333 A+B=633 A+B=23
The value of A+B is 23.
