Question
Question: Select an option...
Select an option
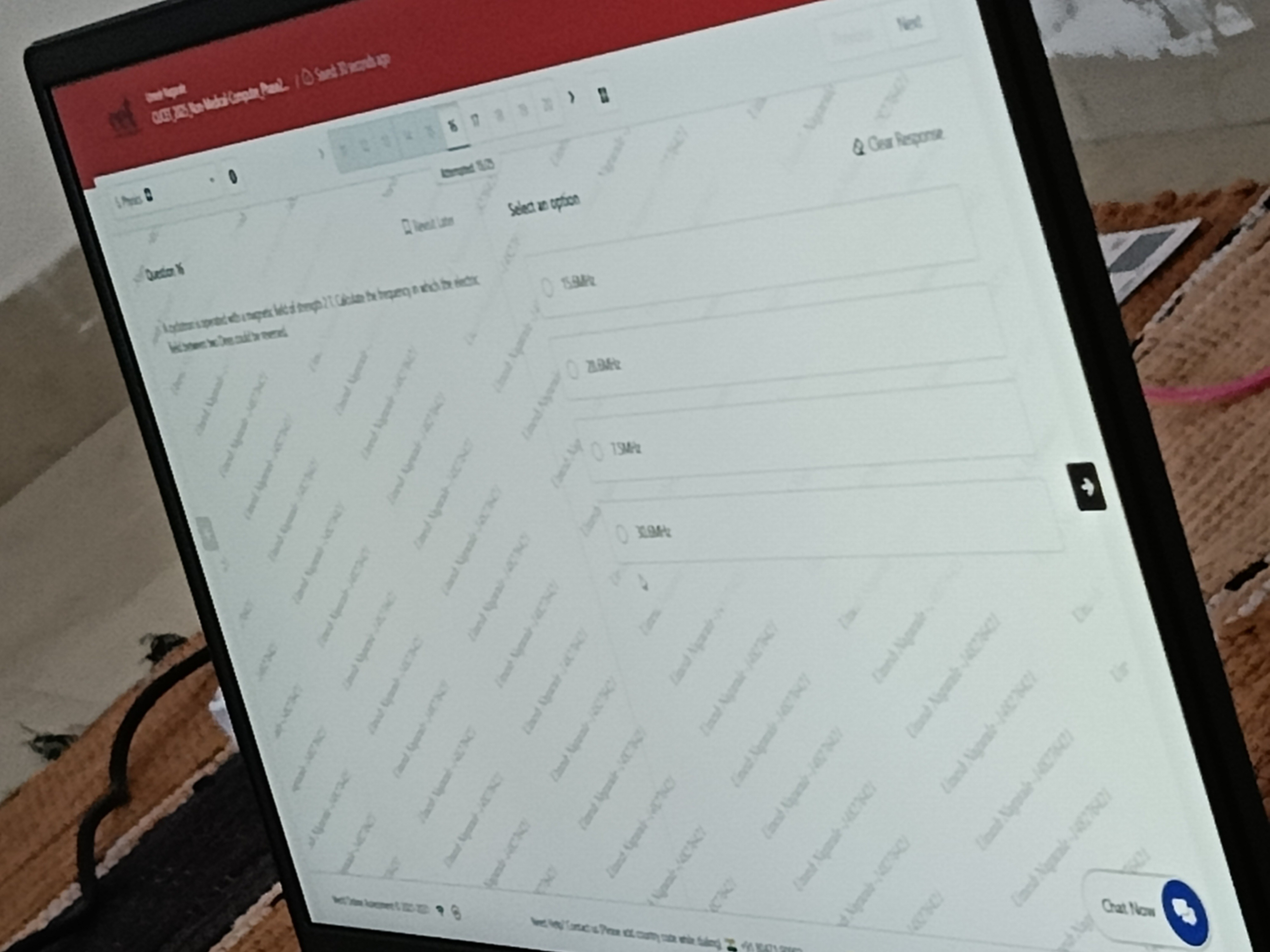
15.9MHz
28.8MHz
7.5MHz
35.9MHz
7.5MHz
Solution
The problem asks to calculate the frequency at which the electric field between the dees of a cyclotron should be reversed, given a magnetic field strength of 1.0 T. This frequency is known as the cyclotron frequency, and it depends on the charge (q) and mass (m) of the particle being accelerated, and the magnetic field strength (B).
The formula for cyclotron frequency (f) is:
f=2πmqB
The problem does not specify the type of particle being accelerated. However, cyclotrons are typically used to accelerate charged particles like protons, deuterons, or alpha particles. Let's calculate the frequency for these common particles and compare with the given options.
We will use the following standard values for constants:
- Charge of electron/proton (e) = 1.602×10−19 C
- Mass of proton (mp) = 1.672×10−27 kg
- Mass of deuteron (md) ≈2×mp=3.344×10−27 kg (charge is e)
- Mass of alpha particle (mα) ≈4×mp=6.688×10−27 kg (charge is 2e)
- Magnetic field strength (B) = 1.0 T
- π≈3.14159
1. For a Proton:
fp=2πmpeB=2×3.14159×(1.672×10−27 kg)(1.602×10−19 C)×(1.0 T)
fp=10.505×10−271.602×10−19
fp=0.1525×108 Hz
fp=15.25 MHz
Comparing this to the options, 15.9 MHz is the closest for a proton. The difference is 15.9−15.25=0.65 MHz, which is a relative difference of about 4.3%.
2. For a Deuteron:
A deuteron has the same charge as a proton (e) but approximately twice the mass (md≈2mp).
fd=2πmdeB=2π(2mp)eB=21fp
fd=21×15.25 MHz
fd=7.625 MHz
Comparing this to the options, 7.5 MHz is very close to 7.625 MHz. The difference is 7.625−7.5=0.125 MHz, which is a relative difference of about 1.6%.
3. For an Alpha Particle:
An alpha particle has twice the charge of a proton (2e) and approximately four times the mass (mα≈4mp).
fα=2π(4mp)(2e)B=8πmp2eB=4πmpeB=21fp
fα=21×15.25 MHz
fα=7.625 MHz
Similar to a deuteron, an alpha particle also yields a frequency of 7.625 MHz. This is also very close to 7.5 MHz.
Conclusion:
While a proton is a common particle accelerated in a cyclotron, the calculated frequency of 15.25 MHz has a noticeable deviation from the closest option (15.9 MHz). However, for a deuteron or an alpha particle, the calculated frequency of 7.625 MHz is a much better fit for the option 7.5 MHz, with a significantly smaller percentage difference. In such multiple-choice questions where the particle is not specified, the option that best fits the calculation for a plausible particle is usually the intended answer.
Given the much closer match, it is highly probable that the question intends for a deuteron or an alpha particle to be the accelerated particle.
