Solveeit Logo
Login

Question

Question: Find the work done (in J) by $\overrightarrow{F} = (y\hat{i} - x\hat{j})N$ along the closed path sho...

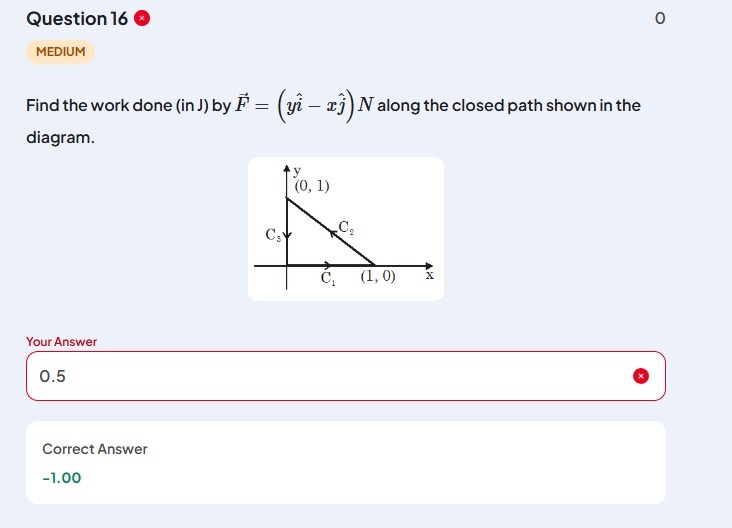
Find the work done (in J) by F→=(yi^−xj^)N\overrightarrow{F} = (y\hat{i} - x\hat{j})N along the closed path shown in the diagram.

Answer

-1.00

Explanation

Solution

The work done by the force F→=(yi^−xj^)\overrightarrow{F} = (y\hat{i} - x\hat{j}) along a path is given by the line integral W=∫CF→⋅dr→W = \int_C \overrightarrow{F} \cdot d\overrightarrow{r}.

Here, dr→=dxi^+dyj^d\overrightarrow{r} = dx\hat{i} + dy\hat{j}. So, F→⋅dr→=(yi^−xj^)⋅(dxi^+dyj^)=y dx−x dy\overrightarrow{F} \cdot d\overrightarrow{r} = (y\hat{i} - x\hat{j}) \cdot (dx\hat{i} + dy\hat{j}) = y\,dx - x\,dy.

The path is a closed triangle with vertices O(0, 0), A(1, 0), and B(0, 1), traversed in the order O to A (C1C_1), A to B (C2C_2), and B to O (C3C_3).

  1. Path C1C_1: From O(0, 0) to A(1, 0). Along this path, y=0y = 0 and dy=0dy = 0. xx goes from 0 to 1. W1=∫C1(y dx−x dy)=∫x=0x=1(0 dx−x⋅0)=∫010 dx=0W_1 = \int_{C_1} (y\,dx - x\,dy) = \int_{x=0}^{x=1} (0\,dx - x \cdot 0) = \int_{0}^{1} 0\,dx = 0.

  2. Path C2C_2: From A(1, 0) to B(0, 1). This is a line segment connecting (1, 0) and (0, 1). The equation of the line passing through these points is x1+y1=1\frac{x}{1} + \frac{y}{1} = 1, or x+y=1x + y = 1. Thus, y=1−xy = 1 - x, and dy=−dxdy = -dx. As we move from A to B, xx goes from 1 to 0. W2=∫C2(y dx−x dy)=∫x=1x=0((1−x) dx−x(−dx))=∫10(1−x+x) dx=∫101 dx=[x]10=0−1=−1W_2 = \int_{C_2} (y\,dx - x\,dy) = \int_{x=1}^{x=0} ((1-x)\,dx - x(-dx)) = \int_{1}^{0} (1-x+x)\,dx = \int_{1}^{0} 1\,dx = [x]_{1}^{0} = 0 - 1 = -1.

  3. Path C3C_3: From B(0, 1) to O(0, 0). Along this path, x=0x = 0 and dx=0dx = 0. yy goes from 1 to 0. W3=∫C3(y dx−x dy)=∫y=1y=0(y⋅0−0 dy)=∫100 dy=0W_3 = \int_{C_3} (y\,dx - x\,dy) = \int_{y=1}^{y=0} (y \cdot 0 - 0\,dy) = \int_{1}^{0} 0\,dy = 0.

The total work done along the closed path is the sum of the work done along each segment: W=W1+W2+W3=0+(−1)+0=−1W = W_1 + W_2 + W_3 = 0 + (-1) + 0 = -1 J.

Alternatively, we can use Green's Theorem. For a force field F→(x,y)=P(x,y)i^+Q(x,y)j^\overrightarrow{F}(x, y) = P(x, y)\hat{i} + Q(x, y)\hat{j}, the work done along a positively oriented closed curve C enclosing a region R is given by ∮C(P dx+Q dy)=∬R(∂Q∂x−∂P∂y) dA\oint_C (P\,dx + Q\,dy) = \iint_R \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\,dA.

Here, P(x,y)=yP(x, y) = y and Q(x,y)=−xQ(x, y) = -x.

∂P∂y=∂∂y(y)=1\frac{\partial P}{\partial y} = \frac{\partial}{\partial y}(y) = 1.

∂Q∂x=∂∂x(−x)=−1\frac{\partial Q}{\partial x} = \frac{\partial}{\partial x}(-x) = -1.

∂Q∂x−∂P∂y=−1−1=−2\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = -1 - 1 = -2.

The region R is the triangle with vertices (0, 0), (1, 0), and (0, 1). The area of this triangle is 12×base×height=12×1×1=12\frac{1}{2} \times base \times height = \frac{1}{2} \times 1 \times 1 = \frac{1}{2}.

The work done is ∬R(−2) dA=−2∬R dA=−2×Area(R)=−2×12=−1\iint_R (-2)\,dA = -2 \iint_R \,dA = -2 \times \text{Area}(R) = -2 \times \frac{1}{2} = -1 J.

The path is traversed in the counterclockwise direction, which is the positive orientation for Green's Theorem.