Question

1 moles of the He gas undergoes a cyclic process MNOPM as shown in T - V diagram. Temperature of gas in state M is 300 K.

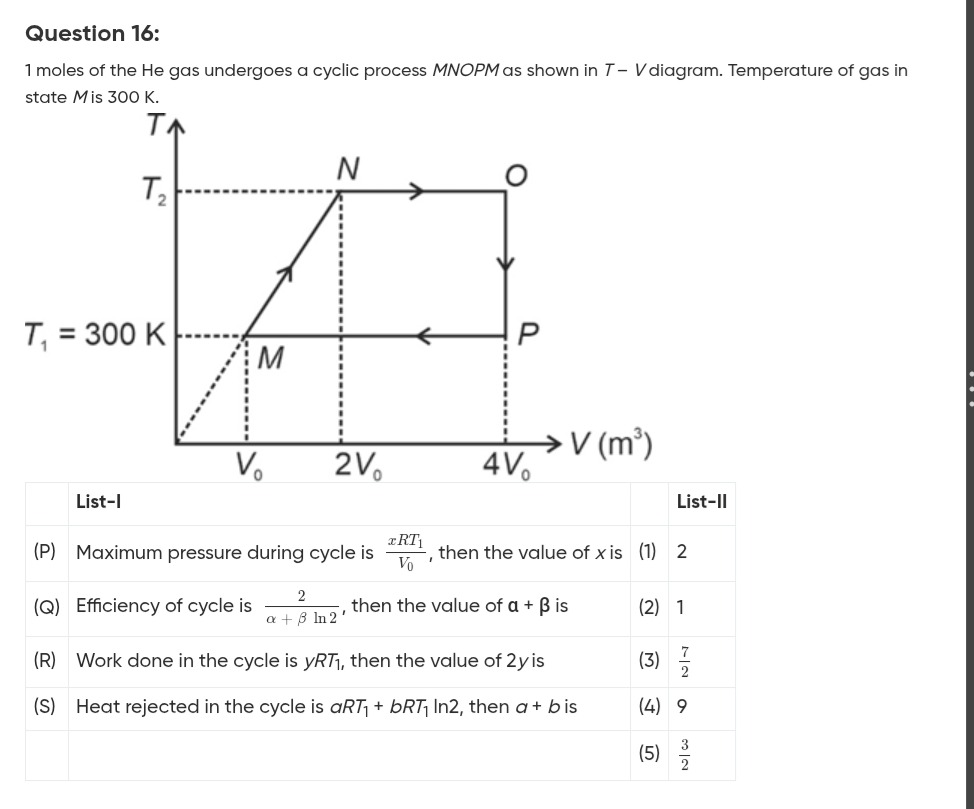
• A. Maximum pressure during cycle is $\frac{xRT_1}{V_0}$, then the value of x is
• B. Efficiency of cycle is $\frac{2}{\alpha + \beta \ln 2}$, then the value of $\alpha + \beta$ is
• C. Work done in the cycle is $yRT_1$, then the value of 2y is
• D. Heat rejected in the cycle is $aRT_1 + bRT_1 \ln 2$, then a + b is

Answer 1

(P) - (2), (Q) - (4), (R) - (1), (S) - (3)

Answer 2

The given process is a cyclic process MNOPM for 1 mole of He gas (monoatomic, $C_V = \frac{3}{2}R$, $C_P = \frac{5}{2}R$). The temperature at state M is $T_1 = 300$ K.

From the T-V diagram:

State M: $(V_0, T_1)$

State N: $(2V_0, T_2)$

State O: $(4V_0, T_2)$

State P: $(4V_0, T_1)$

Process M-N is a straight line in T-V diagram passing through the origin if extended, so $T \propto V$. Thus, $\frac{T_M}{V_M} = \frac{T_N}{V_N}$, so $\frac{T_1}{V_0} = \frac{T_2}{2V_0}$, which gives $T_2 = 2T_1$.

Also, $P = \frac{RT}{V}$. Since $\frac{T}{V}$ is constant, $P$ is constant. Process M-N is isobaric.

$P_{MN} = \frac{RT_M}{V_M} = \frac{RT_1}{V_0}$.

Process N-O is isothermal at $T_2 = 2T_1$.

Process O-P is isochoric at $V_O = 4V_0$.

Process P-M is isothermal at $T_1$.

Pressures at the states:

$P_M = \frac{RT_1}{V_0}$

$P_N = \frac{RT_2}{2V_0} = \frac{R(2T_1)}{2V_0} = \frac{RT_1}{V_0}$

$P_O = \frac{RT_2}{4V_0} = \frac{R(2T_1)}{4V_0} = \frac{RT_1}{2V_0}$

$P_P = \frac{RT_1}{4V_0}$

(P) Maximum pressure during cycle.

Pressures at the vertices are $P_M = P_N = \frac{RT_1}{V_0}$, $P_O = \frac{RT_1}{2V_0}$, $P_P = \frac{RT_1}{4V_0}$.

During N-O (isothermal expansion), $P = \frac{2RT_1}{V}$, pressure decreases from $P_N$ to $P_O$.

During O-P (isochoric cooling), $P = \frac{RT}{4V_0}$, pressure decreases from $P_O$ to $P_P$.

During P-M (isothermal compression), $P = \frac{RT_1}{V}$, pressure increases from $P_P$ to $P_M$.

Maximum pressure is $\frac{RT_1}{V_0}$. Given maximum pressure is $\frac{xRT_1}{V_0}$, so $x=1$.

(P) matches with (2).

(Q) Efficiency of cycle $\eta = \frac{W_{cycle}}{Q_{in}}$.

Work done in each process:

$W_{MN} = P_{MN}(V_N - V_M) = \frac{RT_1}{V_0}(2V_0 - V_0) = RT_1$.

$W_{NO} = nRT_N \ln(\frac{V_O}{V_N}) = R(2T_1) \ln(\frac{4V_0}{2V_0}) = 2RT_1 \ln 2$.

$W_{OP} = 0$ (isochoric).

$W_{PM} = nRT_P \ln(\frac{V_M}{V_P}) = RT_1 \ln(\frac{V_0}{4V_0}) = RT_1 \ln(4^{-1}) = -RT_1 \ln 4 = -2RT_1 \ln 2$.

$W_{cycle} = W_{MN} + W_{NO} + W_{OP} + W_{PM} = RT_1 + 2RT_1 \ln 2 + 0 - 2RT_1 \ln 2 = RT_1$.

Heat transfer in each process ($n=1$):

$Q_{MN} = nC_P(T_N - T_M) = 1 \times \frac{5}{2}R(2T_1 - T_1) = \frac{5}{2}RT_1$ (heat absorbed).

$Q_{NO} = W_{NO} = 2RT_1 \ln 2$ (heat absorbed, isothermal expansion).

$Q_{OP} = nC_V(T_P - T_O) = 1 \times \frac{3}{2}R(T_1 - 2T_1) = -\frac{3}{2}RT_1$ (heat rejected).

$Q_{PM} = W_{PM} = -2RT_1 \ln 2$ (heat rejected, isothermal compression).

Heat absorbed $Q_{in} = Q_{MN} + Q_{NO} = \frac{5}{2}RT_1 + 2RT_1 \ln 2$.

Efficiency $\eta = \frac{W_{cycle}}{Q_{in}} = \frac{RT_1}{\frac{5}{2}RT_1 + 2RT_1 \ln 2} = \frac{1}{\frac{5}{2} + 2 \ln 2} = \frac{2}{5 + 4 \ln 2}$.

Given efficiency is $\frac{2}{\alpha + \beta \ln 2}$. Comparing, $\alpha = 5, \beta = 4$.

$\alpha + \beta = 5 + 4 = 9$.

(Q) matches with (4).

(R) Work done in the cycle is $yRT_1$.

We found $W_{cycle} = RT_1$. Given $W_{cycle} = yRT_1$, so $y=1$.

We need to find $2y = 2 \times 1 = 2$.

(R) matches with (1).

(S) Heat rejected in the cycle is $aRT_1 + bRT_1 \ln 2$.

Heat rejected $Q_{rejected} = |Q_{OP}| + |Q_{PM}| = |-\frac{3}{2}RT_1| + |-2RT_1 \ln 2| = \frac{3}{2}RT_1 + 2RT_1 \ln 2$.

Given heat rejected is $aRT_1 + bRT_1 \ln 2$. Comparing, $a = \frac{3}{2}$ and $b = 2$.

$a+b = \frac{3}{2} + 2 = \frac{3}{2} + \frac{4}{2} = \frac{7}{2}$.

(S) matches with (3).

Summary of matches:

(P) - (2)

(Q) - (4)

(R) - (1)

(S) - (3)

Explanation of the solution:

1. Determine the coordinates (V, T) for each state M, N, O, P from the T-V diagram.

2. Identify the type of process for each step (M-N, N-O, O-P, P-M) based on the T-V diagram.

3. Calculate the pressure at each state using the ideal gas law $PV=nRT$.

4. For (P), find the maximum pressure during the cycle by examining the pressures at the states and how pressure changes during each process. Compare with the given expression to find $x$.

5. For (Q), calculate the work done and heat absorbed/rejected in each process. Calculate the net work done in the cycle and the total heat absorbed. Calculate the efficiency $\eta = \frac{W_{cycle}}{Q_{in}}$. Compare with the given expression to find $\alpha$ and $\beta$, then calculate $\alpha + \beta$.

6. For (R), the work done in the cycle is already calculated in step 5. Compare with the given expression to find $y$, then calculate $2y$.

7. For (S), identify the processes where heat is rejected. Calculate the magnitude of heat rejected in these processes and sum them up. Compare with the given expression to find $a$ and $b$, then calculate $a+b$.

8. Match the calculated values with the options in List-II.