Question
Question: If $x^k + y^k = a^k (a, k > 0)$ and $\frac{dy}{dx} + (\frac{y}{x})^{\frac{1}{2}} = 0$ then k has the...
If xk+yk=ak(a,k>0) and dxdy+(xy)21=0 then k has the value:
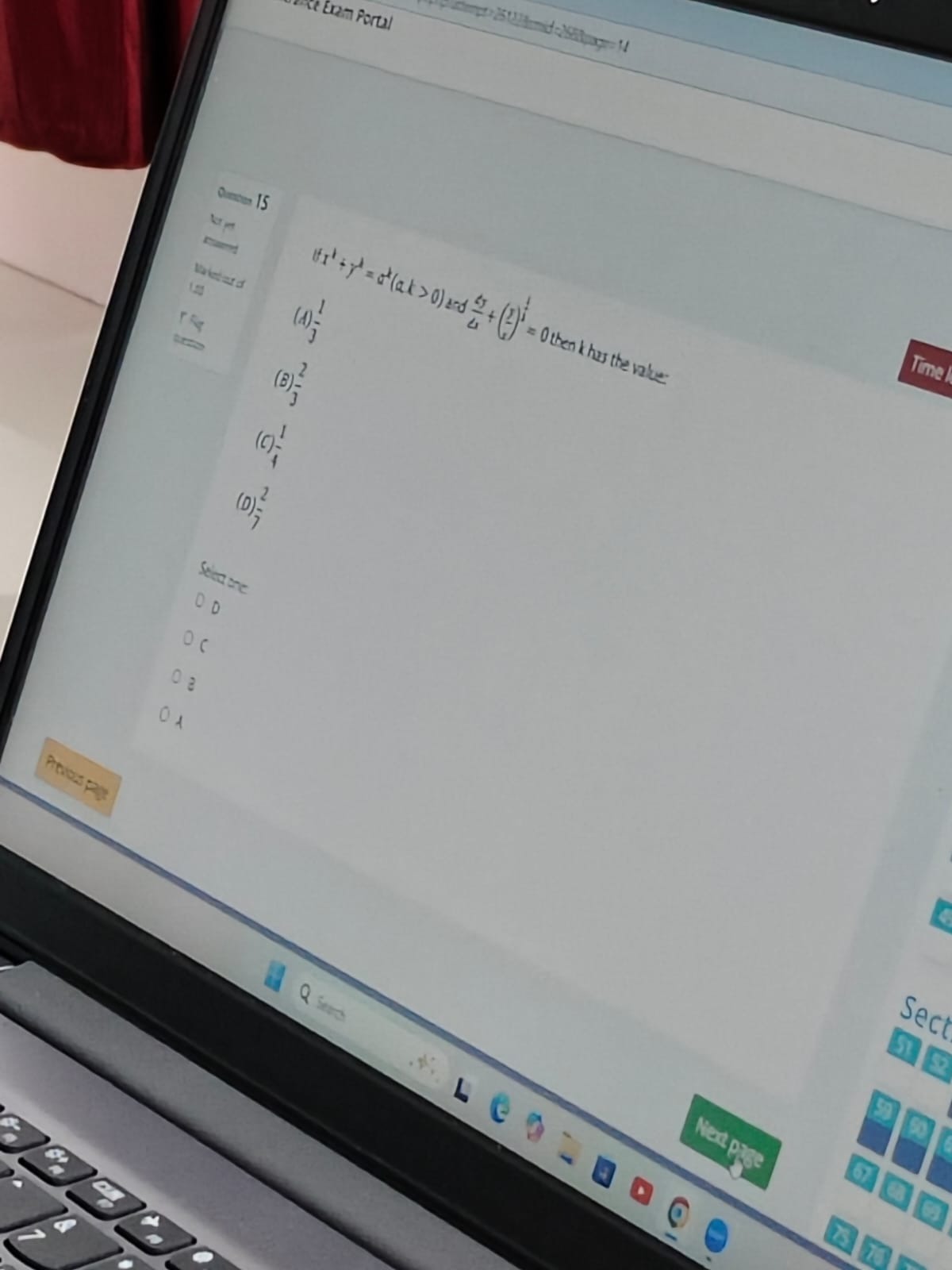
31
32
41
72
The calculated value of k is 21. However, this value is not among the given options. There might be an error in the question or the options provided.
Solution
To find the value of k, we use the given equations:
- xk+yk=ak (where a,k>0)
- dxdy+(xy)21=0
Step 1: Differentiate the first equation with respect to x.
Given xk+yk=ak. Differentiating both sides implicitly with respect to x:
dxd(xk)+dxd(yk)=dxd(ak)
Using the power rule dxd(un)=nun−1dxdu:
kxk−1+kyk−1dxdy=0
Since k>0, we can divide the entire equation by k:
xk−1+yk−1dxdy=0
Now, solve for dxdy:
yk−1dxdy=−xk−1
dxdy=−yk−1xk−1
dxdy=−(yx)k−1
Step 2: Use the second given equation to express dxdy.
Given dxdy+(xy)21=0.
Solving for dxdy:
dxdy=−(xy)21
Step 3: Equate the two expressions for dxdy.
From Step 1: dxdy=−(yx)k−1
From Step 2: dxdy=−(xy)21
Equating them:
−(yx)k−1=−(xy)21
Multiply by -1:
(yx)k−1=(xy)21
Step 4: Solve for k by comparing exponents.
We can rewrite (xy)21 as ((yx)−1)21=(yx)−21.
So, the equation becomes:
(yx)k−1=(yx)−21
For the bases to be equal, the exponents must be equal:
k−1=−21
k=1−21
k=22−21
k=21
The calculated value of k is 21. However, this value is not present in any of the given options. This suggests a potential error in the question's options or the question itself.
