Question

If $x + \frac{1}{x} = 2 \cos \theta$, then x is equal to

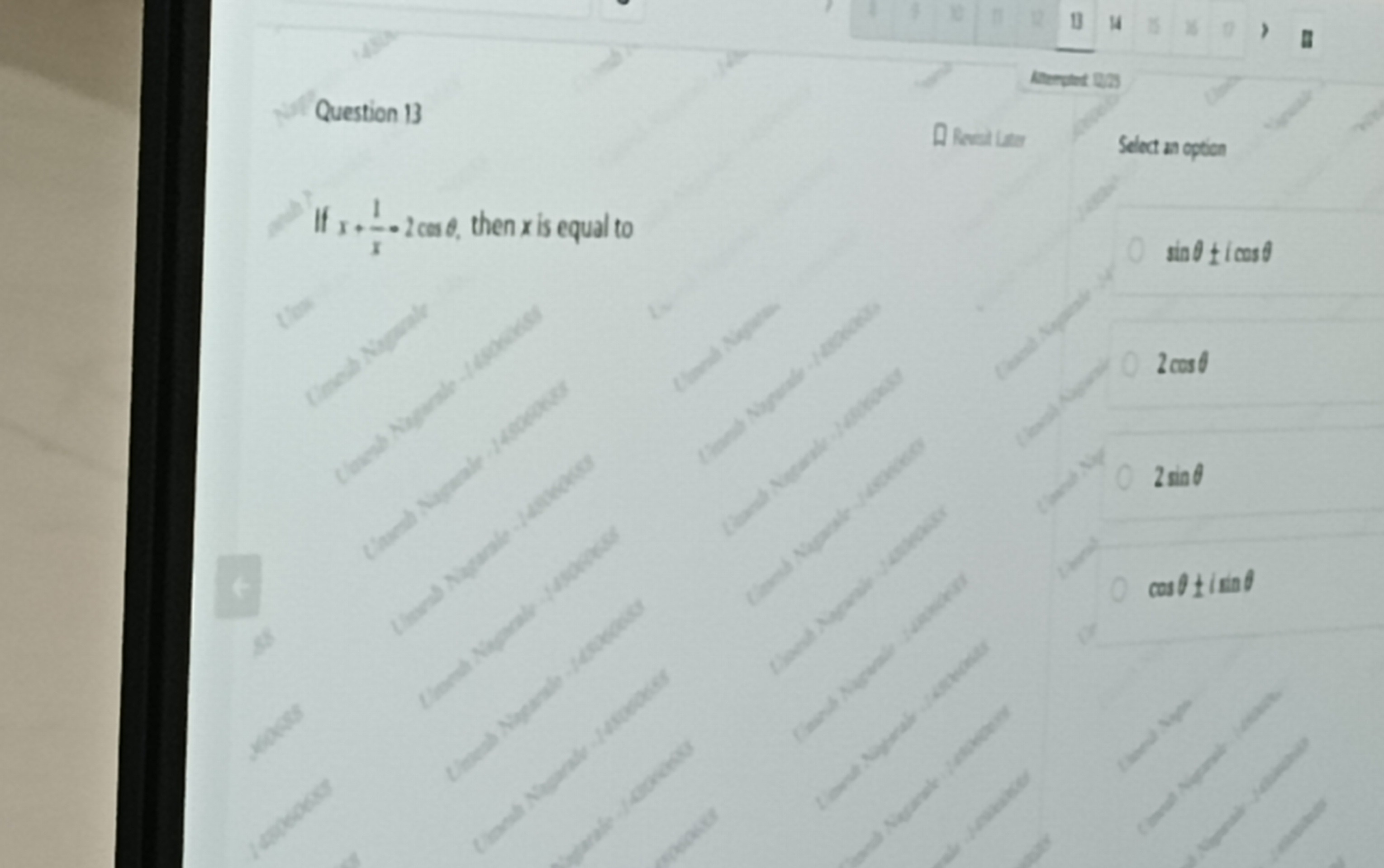
• A. $\sin \theta \pm i \cos \theta$
• B. $2 \cos \theta$
• C. $2 \sin \theta$
• D. $\cos \theta \pm i \sin \theta$

Answer 1

Answer: (D)

$\cos \theta \pm i \sin \theta$

Answer 2

The given equation $x + \frac{1}{x} = 2 \cos \theta$ is transformed into a quadratic equation $x^2 - (2 \cos \theta) x + 1 = 0$. Using the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, we substitute $a=1$, $b=-2 \cos \theta$, and $c=1$. This yields $x = \frac{2 \cos \theta \pm \sqrt{4 \cos^2 \theta - 4}}{2}$. Simplifying the term under the square root using the identity $\cos^2 \theta - 1 = -\sin^2 \theta$, we get $x = \frac{2 \cos \theta \pm \sqrt{-4 \sin^2 \theta}}{2}$. Introducing the imaginary unit $i = \sqrt{-1}$, this simplifies to $x = \frac{2 \cos \theta \pm 2i \sin \theta}{2}$, which further simplifies to $x = \cos \theta \pm i \sin \theta$.