Question

200 mL, 0.6 M $CuSO_4$ solution is electrolyzed by platinum electrodes for 1447.5 sec by steady current of 5A (50% efficiency). The concentration of solution after electrolysis is x $\times$ $10^{-1}$ M. The value of x is (nearest integer)

Answer 1

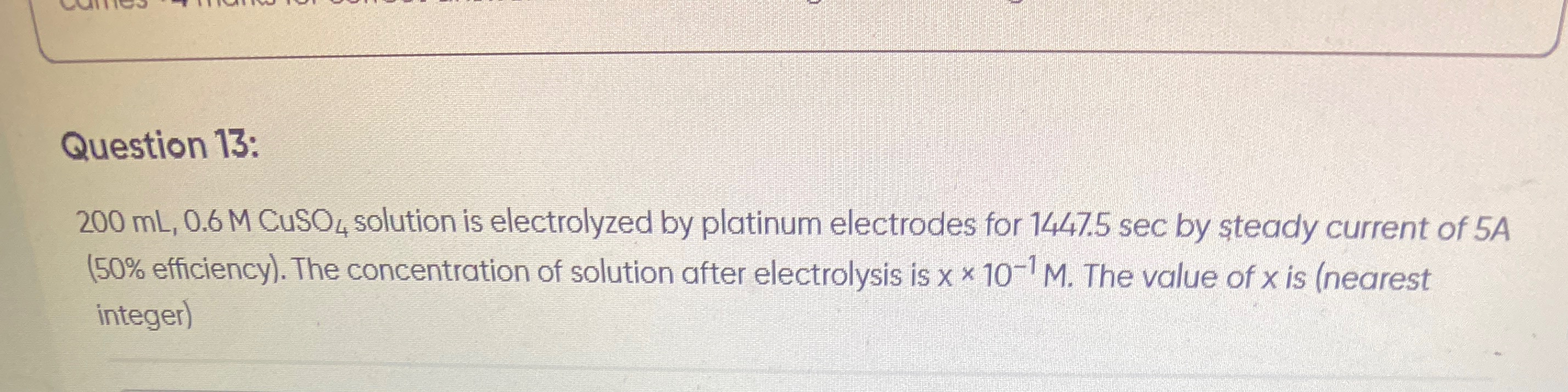
5

Answer 2

The problem asks us to determine the final concentration of $CuSO_4$ solution after electrolysis.

Here's a step-by-step solution:

1. Calculate initial moles of $CuSO_4$: The initial volume of the solution is 200 mL = 0.2 L. The initial molarity is 0.6 M. Initial moles of $CuSO_4 = \text{Molarity} \times \text{Volume} = 0.6 \text{ mol/L} \times 0.2 \text{ L} = 0.12 \text{ mol}$.

2. Calculate the total charge passed: The current (I) is 5 A. The time (t) is 1447.5 s. Total charge ($Q_{total}$) = $I \times t = 5 \text{ A} \times 1447.5 \text{ s} = 7237.5 \text{ C}$.

3. Calculate the effective charge (considering efficiency): The efficiency of electrolysis is 50% (0.5). Effective charge ($Q_{effective}$) = $Q_{total} \times \text{Efficiency} = 7237.5 \text{ C} \times 0.5 = 3618.75 \text{ C}$.

4. Calculate the moles of electrons passed: We use Faraday's constant (F = 96485 C/mol $e^-$). Moles of electrons ($n_{e^-}$) = $\frac{Q_{effective}}{F} = \frac{3618.75 \text{ C}}{96485 \text{ C/mol } e^-} \approx 0.037505 \text{ mol } e^-$.

5. Determine the moles of $Cu^{2+}$ consumed: At the cathode, the reaction is the reduction of copper ions: $Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)$ From the stoichiometry, 2 moles of electrons are required to deposit 1 mole of Cu (or consume 1 mole of $Cu^{2+}$). Moles of $Cu^{2+}$ consumed = $\frac{\text{Moles of } e^-}{2} = \frac{0.037505 \text{ mol}}{2} \approx 0.0187525 \text{ mol}$.

6. Calculate the final moles of $CuSO_4$: Since $CuSO_4$ dissociates into $Cu^{2+}$ and $SO_4^{2-}$, the consumption of $Cu^{2+}$ ions directly reduces the moles of $CuSO_4$ in the solution. Final moles of $CuSO_4 = \text{Initial moles} - \text{Moles of } Cu^{2+} \text{ consumed}$ Final moles of $CuSO_4 = 0.12 \text{ mol} - 0.0187525 \text{ mol} = 0.1012475 \text{ mol}$.

7. Calculate the final concentration of $CuSO_4$: The volume of the solution remains 0.2 L (assuming no significant volume change due to deposition). Final concentration = $\frac{\text{Final moles}}{\text{Volume}} = \frac{0.1012475 \text{ mol}}{0.2 \text{ L}} = 0.5062375 \text{ M}$.

8. Express the concentration in the required format: The question asks for the concentration in the format $x \times 10^{-1}$ M. $0.5062375 \text{ M} = 5.062375 \times 10^{-1} \text{ M}$. Therefore, $x = 5.062375$.

9. Find the nearest integer value of x: The nearest integer to 5.062375 is 5.

The final answer is $\boxed{5}$.

Explanation of the solution:

1. Calculated initial moles of $CuSO_4$ using given volume and molarity.
2. Calculated total charge passed using current and time.
3. Adjusted total charge for 50% efficiency to find effective charge used for electrolysis.
4. Used Faraday's first law to convert effective charge to moles of electrons.
5. Used the stoichiometry of $Cu^{2+} + 2e^- \rightarrow Cu(s)$ to find moles of $Cu^{2+}$ consumed from moles of electrons.
6. Subtracted consumed moles of $Cu^{2+}$ from initial moles of $CuSO_4$ to get final moles.
7. Calculated final concentration by dividing final moles by the initial volume (assuming constant volume).
8. Expressed the final concentration in the specified format ($x \times 10^{-1}$ M) and rounded x to the nearest integer.