Question

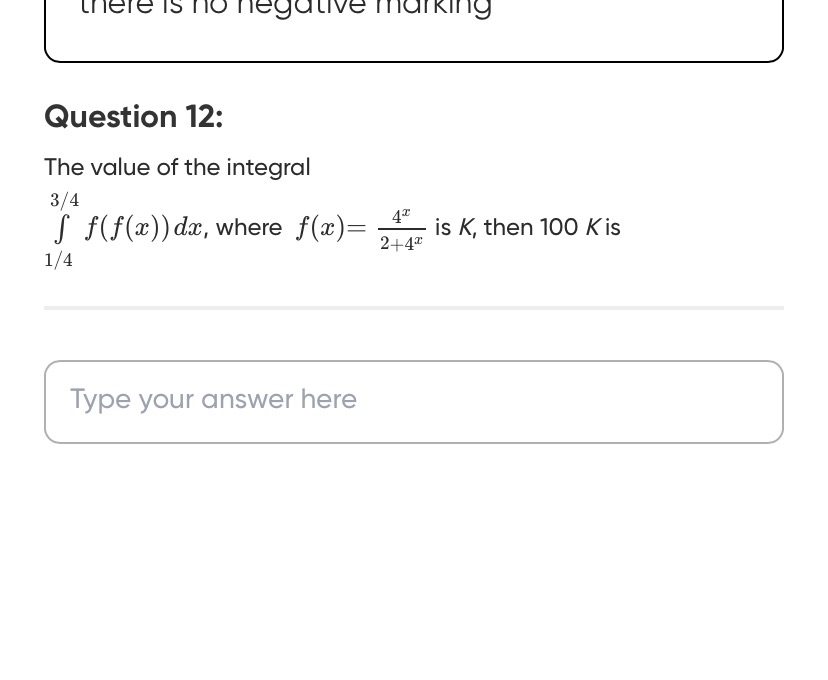
The value of the integral $\int_{1/4}^{3/4} f(f(x))\, dx$, where $f(x)=\frac{4^x}{2+4^x}$ is $K$, then 100 $K$ is

Answer 1

25

Answer 2

To evaluate the integral $K = \int_{1/4}^{3/4} f(f(x))\, dx$, where $f(x)=\frac{4^x}{2+4^x}$, we first analyze the properties of the function $f(x)$.

Step 1: Analyze the function $f(x)$

The given function is $f(x) = \frac{4^x}{2+4^x}$. Let's check the property $f(x) + f(1-x)$. $f(1-x) = \frac{4^{1-x}}{2+4^{1-x}} = \frac{4/4^x}{2+4/4^x} = \frac{4/4^x}{(2 \cdot 4^x + 4)/4^x} = \frac{4}{2 \cdot 4^x + 4} = \frac{2}{4^x+2}$. Now, add $f(x)$ and $f(1-x)$: $f(x) + f(1-x) = \frac{4^x}{2+4^x} + \frac{2}{2+4^x} = \frac{4^x+2}{2+4^x} = 1$. So, we have the important property: $f(x) + f(1-x) = 1$. This implies $f(1-x) = 1 - f(x)$.

Step 2: Determine the range of $f(x)$

For $x \in \mathbb{R}$, $4^x > 0$. $f(x) = \frac{4^x}{2+4^x}$. Since $4^x > 0$, $f(x) > 0$. Also, $f(x) = \frac{4^x}{2+4^x} = \frac{1}{2/4^x + 1}$. Since $2/4^x > 0$, we have $2/4^x + 1 > 1$. Therefore, $0 < \frac{1}{2/4^x + 1} < 1$. So, the range of $f(x)$ is $(0,1)$.

Step 3: Evaluate the integral $K$

Let $K = \int_{1/4}^{3/4} f(f(x))\, dx$. We use the property of definite integrals: $\int_a^b g(x) dx = \int_a^b g(a+b-x) dx$. Here, $a=1/4$ and $b=3/4$, so $a+b = 1/4 + 3/4 = 1$. Applying this property to $K$: $K = \int_{1/4}^{3/4} f(f(1-x))\, dx$.

From Step 1, we know $f(1-x) = 1-f(x)$. Substitute this into the integral: $K = \int_{1/4}^{3/4} f(1-f(x))\, dx$.

Now, let $y = f(x)$. From Step 2, we know that $y \in (0,1)$. Since $y \in (0,1)$, $1-y \in (0,1)$. The property $f(z) + f(1-z) = 1$ holds for any $z$ in the domain of $f$. Since $y$ and $1-y$ are in $(0,1)$, which is part of the domain of $f$, we can apply the property for $z=y$: $f(y) + f(1-y) = 1 \implies f(1-y) = 1-f(y)$. Replacing $y$ with $f(x)$, we get $f(1-f(x)) = 1-f(f(x))$.

Substitute this back into the integral for $K$: $K = \int_{1/4}^{3/4} (1-f(f(x)))\, dx$. Split the integral: $K = \int_{1/4}^{3/4} 1\, dx - \int_{1/4}^{3/4} f(f(x))\, dx$. The second term on the right side is again $K$: $K = [x]_{1/4}^{3/4} - K$. $K = \left(\frac{3}{4} - \frac{1}{4}\right) - K$. $K = \frac{2}{4} - K$. $K = \frac{1}{2} - K$. Now, solve for $K$: $2K = \frac{1}{2}$. $K = \frac{1}{4}$.

Step 4: Calculate $100K$

The question asks for the value of $100K$. $100K = 100 \times \frac{1}{4} = 25$.

The final answer is $\boxed{25}$.