Question

If three capacitors of capacitance C1, C2 and C3 are connected in series then its equivalent is

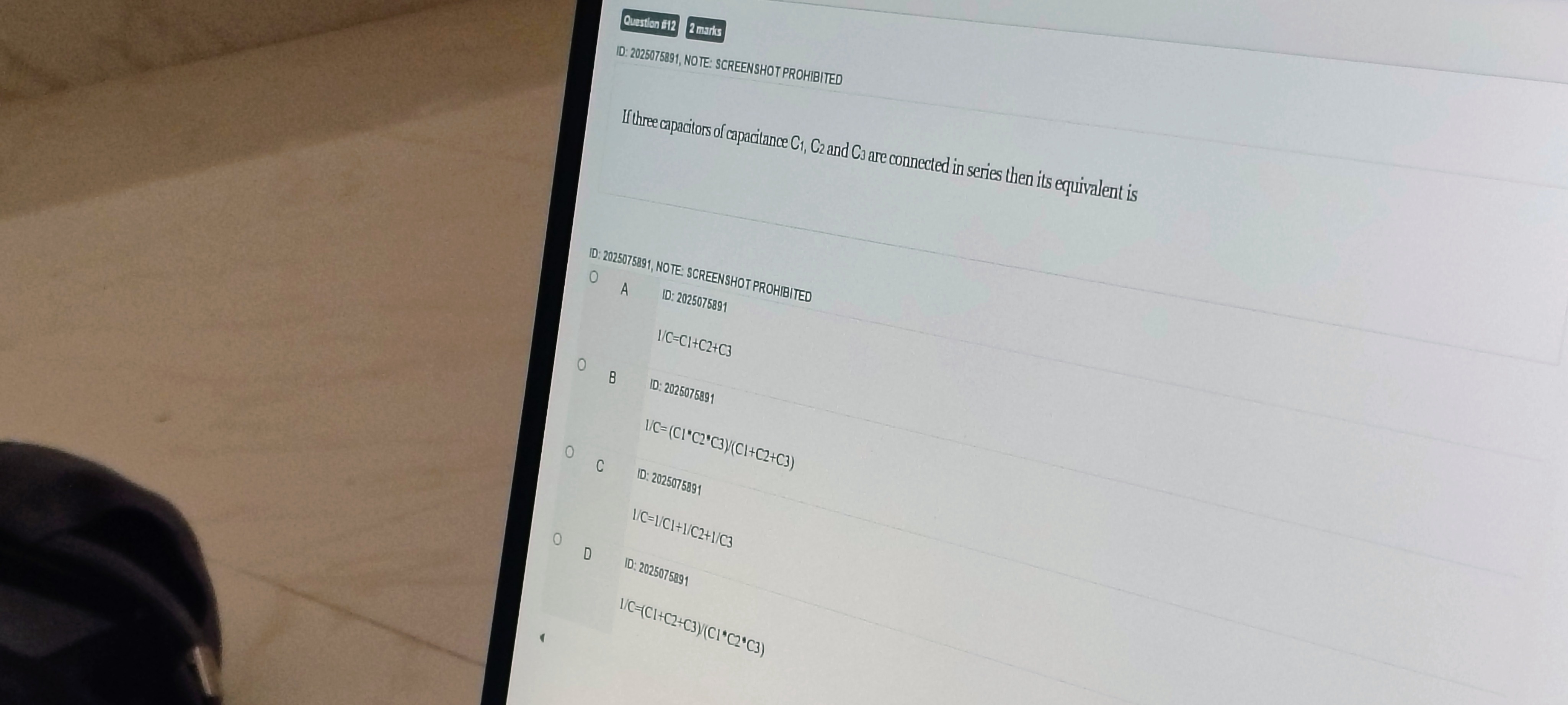
• A. $\frac{1}{C}=C1+C2+C3$
• B. $\frac{1}{C}=\frac{(C1*C2*C3)}{(C1+C2+C3)}$
• C. $\frac{1}{C}=\frac{1}{C1}+\frac{1}{C2}+\frac{1}{C3}$
• D. $\frac{1}{C}=\frac{(C1+C2+C3)}{(C1*C2*C3)}$

Answer 1

Answer: (C)

The equivalent capacitance $C$ of three capacitors $C_1$, $C_2$, and $C_3$ connected in series is given by:

$$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$

Answer 2

When capacitors are connected in series, the reciprocal of the equivalent capacitance is the sum of the reciprocals of the individual capacitances.

For capacitors in series, the total potential difference across the combination is the sum of potential differences across individual capacitors, and the charge on each capacitor is the same.

$V = V_1 + V_2 + V_3$

Since $V = Q/C$, we have:

$Q/C = Q/C_1 + Q/C_2 + Q/C_3$

Dividing by Q (assuming Q is not zero), we get:

$$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$