Question

A current square of side L, carrying current $i$ is placed in x-y plane as shown in which uniform magnetic field $\vec{B}=B_0$ exists at 45° with positive x-axis in x-y plane. The torque upon square is

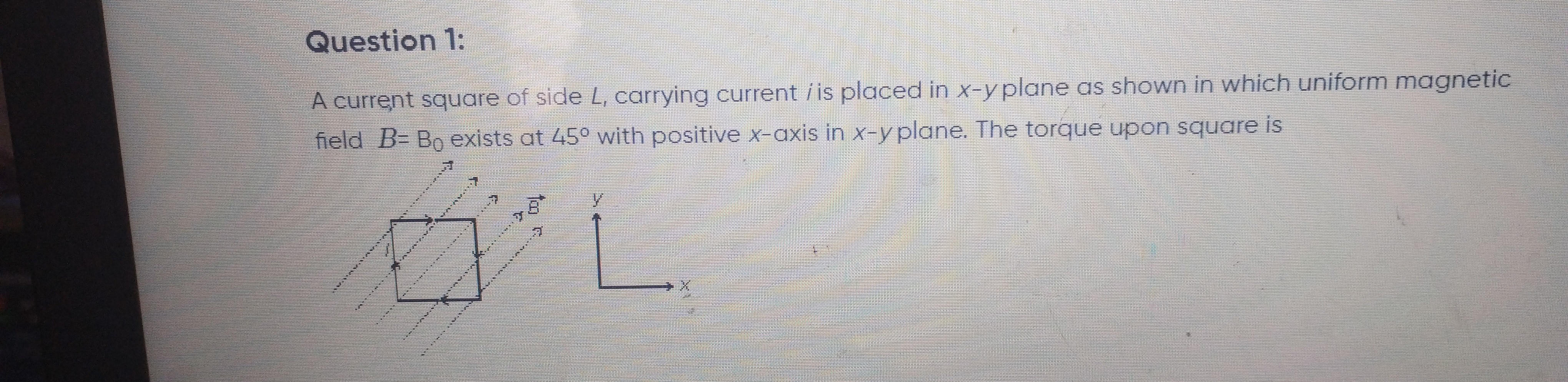
Answer 1

$\frac{iL^2 B_0}{\sqrt{2}} (\hat{i} - \hat{j})$

Answer 2

The torque on a current loop in a magnetic field is given by $\vec{\tau} = \vec{m} \times \vec{B}$. The magnetic dipole moment is $\vec{m} = -iL^2 \hat{k}$ (due to clockwise current). The magnetic field is $\vec{B} = \frac{B_0}{\sqrt{2}} (\hat{i} + \hat{j})$. The torque is $\vec{\tau} = (-iL^2 \hat{k}) \times \left(\frac{B_0}{\sqrt{2}} (\hat{i} + \hat{j})\right) = -iL^2 \frac{B_0}{\sqrt{2}} (\hat{j} - \hat{i}) = iL^2 \frac{B_0}{\sqrt{2}} (\hat{i} - \hat{j})$.