Question

If $\cos^{-1}\left(\frac{y}{b}\right)=\log\left(\frac{x}{n}\right)^n$ prove that $x^2y_{n+2}+(2n+1)xy_{n+1}+2n^2y_n=0$

Answer 1

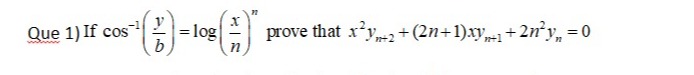
The proof involves differentiating the given relation twice to obtain a second-order differential equation and then applying Leibniz's rule for differentiation $n$ times to arrive at the desired equation.

Answer 2

The given relation is: $\cos^{-1}\left(\frac{y}{b}\right) = n \log\left(\frac{x}{n}\right)$

Differentiating with respect to $x$: $\frac{-1}{\sqrt{1 - (y/b)^2}} \cdot \frac{1}{b} \frac{dy}{dx} = n \cdot \frac{1}{x/n} \cdot \frac{1}{n}$ $\frac{-b}{\sqrt{b^2 - y^2}} \cdot \frac{1}{b} y' = \frac{n}{x} \cdot \frac{1}{n}$ $\frac{-y'}{\sqrt{b^2 - y^2}} = \frac{1}{x}$ $x y' = -\sqrt{b^2 - y^2}$

Squaring both sides: $x^2 (y')^2 = b^2 - y^2$

Differentiating again with respect to $x$: $2x (y')^2 + x^2 \cdot 2y' y'' = -2y y'$ Dividing by $2y'$ (assuming $y' \neq 0$): $x y' + x^2 y'' = -y$ $x^2 y'' + x y' + y = 0$

Let's recheck the first derivative step. $\frac{-y'}{\sqrt{b^2 - y^2}} = \frac{n}{x}$ $x y' = -n \sqrt{b^2 - y^2}$ Squaring both sides: $x^2 (y')^2 = n^2 (b^2 - y^2)$ Differentiating with respect to $x$: $2x (y')^2 + x^2 \cdot 2y' y'' = n^2 (-2y y')$ Dividing by $2y'$: $x y' + x^2 y'' = -n^2 y$ $x^2 y'' + x y' + n^2 y = 0$

Now, differentiate this equation $n$ times using Leibniz's rule: $D^n(uv) = \sum_{k=0}^n \binom{n}{k} u^{(k)} v^{(n-k)}$. Let $y_k = \frac{d^k y}{dx^k}$. $D^n(x^2 y_2) + D^n(x y_1) + D^n(n^2 y) = 0$

1. $D^n(x^2 y_2) = \binom{n}{0} x^2 y_{n+2} + \binom{n}{1} (2x) y_{n+1} + \binom{n}{2} (2) y_n$ $= x^2 y_{n+2} + 2nx y_{n+1} + n(n-1) y_n$

2. $D^n(x y_1) = \binom{n}{0} x y_{n+1} + \binom{n}{1} (1) y_n$ $= x y_{n+1} + n y_n$

3. $D^n(n^2 y) = n^2 y_n$

Summing these: $(x^2 y_{n+2} + 2nx y_{n+1} + n(n-1) y_n) + (x y_{n+1} + n y_n) + n^2 y_n = 0$ $x^2 y_{n+2} + (2nx + x) y_{n+1} + (n^2 - n + n + n^2) y_n = 0$ $x^2 y_{n+2} + (2n+1)x y_{n+1} + (2n^2) y_n = 0$ This proves the required relation.