Question
Question: If $x^2+3x+7=0$ and $ax^2+bx+c=0$ have a common root and $a,b,c \in \mathbb{N}$ then minimum value o...
If x2+3x+7=0 and ax2+bx+c=0 have a common root and a,b,c∈N then minimum value of (a+b+c)
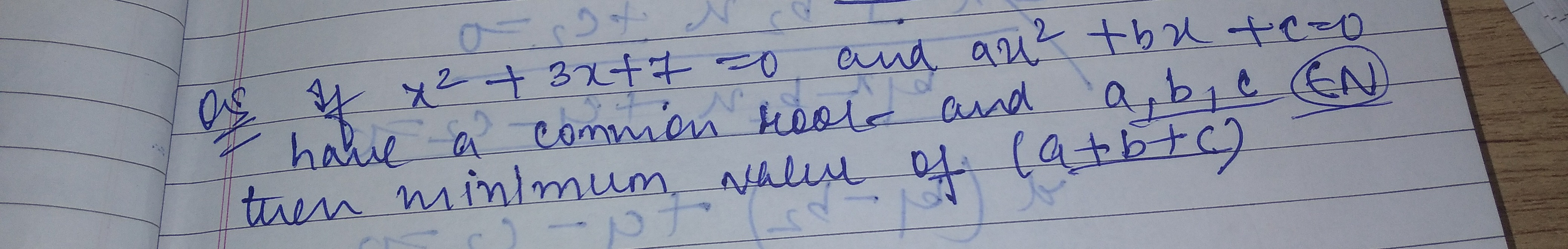
11
Solution
The discriminant of x2+3x+7=0 is D=32−4(1)(7)=9−28=−19<0. The roots are complex. Let γ be the common root. Since γ is a root of x2+3x+7=0, we have γ2+3γ+7=0, which implies γ2=−3γ−7. Since γ is also a root of ax2+bx+c=0, we have aγ2+bγ+c=0. Substituting γ2: a(−3γ−7)+bγ+c=0. Rearranging terms: (b−3a)γ+(c−7a)=0. Since γ is a complex number and a,b,c are real (natural numbers), for this equation to hold, the coefficients of γ and the constant term must both be zero. Thus, b−3a=0⟹b=3a and c−7a=0⟹c=7a. We want to minimize a+b+c=a+3a+7a=11a. Since a,b,c∈N, the smallest possible value for a is 1. When a=1, b=3, and c=7. These are all natural numbers. The minimum value of (a+b+c) is 11×1=11.
