Question

The reaction shown below is the decomposition reaction of hydrogen peroxide.

$2H_2O_2(aq.) \longrightarrow 2H_2O(l) + O_2(g)$

The rate of decomposition can be monitored by measuring the volume of oxygen gas released. The graph shows the results obtained when a solution of hydrogen peroxide decomposed in the presence of a $CuO$ catalyst.

(i) Outline how the initial rate of reaction can be found from the graph.

(ii) Explain how and why the rate of reaction changes with time.

Answer 1

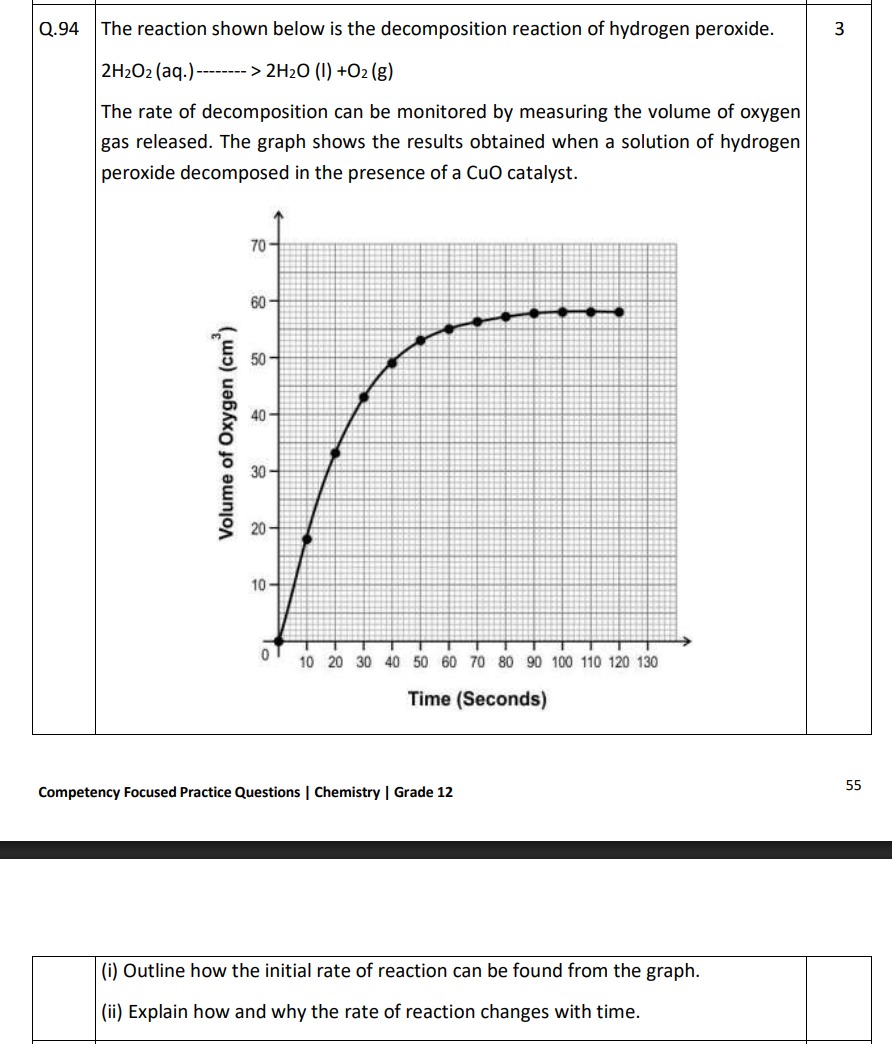
(i) The initial rate of reaction is found by drawing a tangent to the curve at $t=0$ and calculating its slope.

(ii) The rate of reaction decreases with time because as the reaction proceeds, the concentration of the reactant ($H_2O_2$) decreases, leading to a reduction in the frequency of effective collisions between reactant molecules.

Answer 2

The question pertains to the decomposition reaction of hydrogen peroxide and its kinetics, as represented by a graph of oxygen volume produced versus time.

(i) Outline how the initial rate of reaction can be found from the graph.

The rate of reaction at any given time is represented by the gradient (slope) of the tangent to the curve at that specific time. To find the initial rate of reaction:

1. Locate the point on the graph corresponding to time $t = 0$ seconds.
2. Draw a tangent line to the curve at this point ($t=0$).
3. Calculate the gradient (slope) of this tangent line. The slope, $\frac{\Delta \text{Volume of } O_2}{\Delta \text{Time}}$, represents the initial rate of decomposition of hydrogen peroxide.

(ii) Explain how and why the rate of reaction changes with time.

• How the rate changes: Observing the graph, the curve is steepest at the beginning and gradually becomes less steep (flattens out) as time progresses. This indicates that the rate of reaction is fastest at the start and continuously decreases over time until it becomes zero when the reaction is complete (the curve becomes horizontal).
• Why the rate changes: The decomposition of hydrogen peroxide is a reaction that consumes the reactant ($H_2O_2$). As the reaction proceeds, the concentration of hydrogen peroxide decreases. According to collision theory, the rate of a reaction is directly proportional to the concentration of the reactants (assuming other conditions like temperature and catalyst concentration remain constant). As the concentration of $H_2O_2$ decreases, the frequency of effective collisions between $H_2O_2$ molecules (or between $H_2O_2$ molecules and the catalyst surface) diminishes. This reduction in effective collisions leads to a decrease in the reaction rate. Eventually, when all the hydrogen peroxide has decomposed, the reaction stops, and no more oxygen gas is produced.

Explanation of the solution:

(i) The rate of reaction is the change in product concentration (or volume) over time. On a graph of product vs. time, the instantaneous rate is the slope of the tangent at that point. The initial rate is the slope of the tangent at $t=0$.

(ii) The curve flattens over time, indicating a decreasing rate. This is because reactant concentration decreases over time, leading to fewer effective collisions and thus a slower reaction rate.