Solveeit Logo
Login

Question

Question: Let $\Delta = \begin{vmatrix} 1 & x & x^2 \\ x^2 & 1 & x \\ x & x^2 & 1 \end{vmatrix}$, then...

Let Δ=∣1xx2x21xxx21∣\Delta = \begin{vmatrix} 1 & x & x^2 \\ x^2 & 1 & x \\ x & x^2 & 1 \end{vmatrix}, then

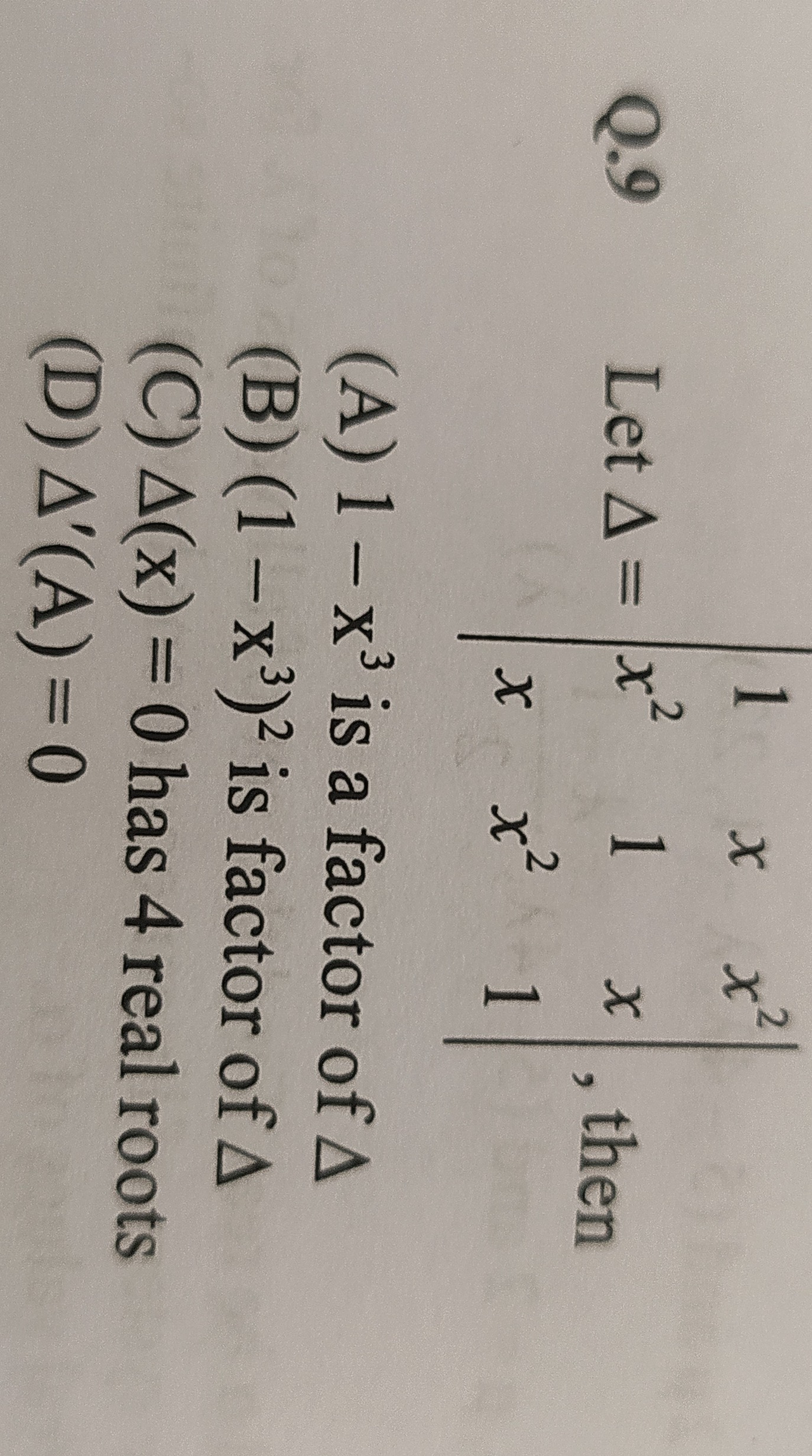
A

1 - x³ is a factor of Δ\Delta

B

(1 - x³)² is factor of Δ\Delta

C

Δ\Delta(x) = 0 has 4 real roots

D

Δ\Delta'(A) = 0

Answer

Options (A), (B), and (D)

Explanation

Solution

We are given

Δ=∣1xx2x21xxx21∣.\Delta = \begin{vmatrix} 1 & x & x^2 \\ x^2 & 1 & x \\ x & x^2 & 1 \end{vmatrix}.

Expanding using the formula for a 3×3 determinant,

Δ=1∣1xx21∣−x∣x2xx1∣+x2∣x21xx2∣.\Delta = 1\begin{vmatrix} 1 & x \\ x^2 & 1 \end{vmatrix} - x\begin{vmatrix} x^2 & x \\ x & 1 \end{vmatrix} + x^2\begin{vmatrix} x^2 & 1 \\ x & x^2 \end{vmatrix}.

Compute each 2×2 determinant:

  • First: ∣1xx21∣=1⋅1−x⋅x2=1−x3.\begin{vmatrix} 1 & x \\ x^2 & 1 \end{vmatrix} = 1\cdot1 - x\cdot x^2 = 1 - x^3.
  • Second: ∣x2xx1∣=x2⋅1−x⋅x=x2−x2=0.\begin{vmatrix} x^2 & x \\ x & 1 \end{vmatrix} = x^2\cdot1 - x\cdot x = x^2 - x^2 = 0.
  • Third: ∣x21xx2∣=x2⋅x2−1⋅x=x4−x.\begin{vmatrix} x^2 & 1 \\ x & x^2 \end{vmatrix} = x^2\cdot x^2 - 1\cdot x = x^4 - x.

Thus,

Δ=1⋅(1−x3)−x⋅0+x2(x4−x)=1−x3+x6−x3=x6−2x3+1.\Delta = 1\cdot(1-x^3) - x\cdot0 + x^2(x^4 - x) = 1-x^3 + x^6 - x^3 = x^6 - 2x^3 + 1.

Notice that

x6−2x3+1=(x3−1)2=(1−x3)2.x^6 - 2x^3 + 1 = (x^3 - 1)^2 = (1-x^3)^2.

Checking the options:

(A) Since Δ=(1−x3)2\Delta = (1-x^3)^2, clearly 1−x31-x^3 is a factor. ✓

(B) (1−x3)2(1-x^3)^2 is exactly Δ\Delta, so it is a factor. ✓

(C) The equation Δ(x)=0\Delta(x) = 0 leads to (1−x3)2=0  ⟹  x3=1(1 - x^3)^2 = 0 \implies x^3 = 1, whose roots are x=1,  −1±i32x = 1,\; \frac{-1 \pm i\sqrt{3}}{2} (only one real root). So 4 real roots is false. ✗

(D) For a repeated (double) root at any xx satisfying x3=1x^3=1, the derivative vanishes. In particular, at the real root x=1x=1,

Δ′(x)=ddx[(1−x3)2]=2(1−x3)(−3x2)=−6x2(1−x3),\Delta'(x) = \frac{d}{dx}[(1-x^3)^2] = 2(1-x^3)(-3x^2) = -6x^2(1-x^3),

and Δ′(1)=−6(1)(0)=0\Delta'(1)= -6(1)(0)=0. ✓