Solveeit Logo
Login

Question

Question: If $\tan(\cot x) = \cot(\tan x)$, [where n ∈ I] then $\sin 2x =$...

If tan⁡(cot⁡x)=cot⁡(tan⁡x)\tan(\cot x) = \cot(\tan x), [where n ∈ I] then sin⁡2x=\sin 2x =

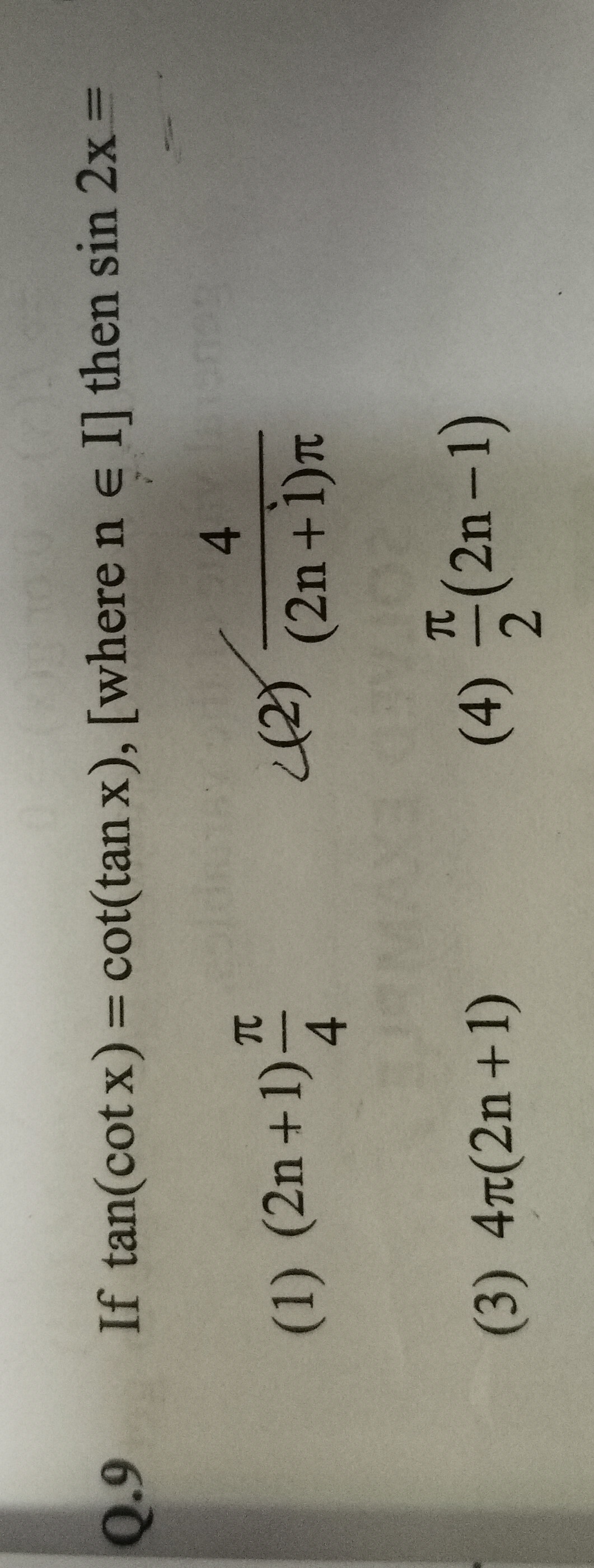
A

π4(2n+1)\frac{\pi}{4}(2n+1)

B

4(2n+1)π\frac{4}{(2n+1)\pi}

C

4π(2n+1)4\pi(2n+1)

D

π2(2n−1)\frac{\pi}{2}(2n-1)

Answer

4(2n+1)π\frac{4}{(2n+1)\pi}

Explanation

Solution

The given equation is tan⁡(cot⁡x)=cot⁡(tan⁡x)\tan(\cot x) = \cot(\tan x). Using the identity cot⁡θ=tan⁡(π2−θ)\cot \theta = \tan(\frac{\pi}{2} - \theta), the equation becomes: tan⁡(cot⁡x)=tan⁡(π2−tan⁡x)\tan(\cot x) = \tan(\frac{\pi}{2} - \tan x)

The general solution for tan⁡A=tan⁡B\tan A = \tan B is A=B+nπA = B + n\pi, where nn is an integer. So, cot⁡x=π2−tan⁡x+nπ\cot x = \frac{\pi}{2} - \tan x + n\pi. Rearranging the terms, we get: cot⁡x+tan⁡x=π2+nπ\cot x + \tan x = \frac{\pi}{2} + n\pi

We know that cot⁡x+tan⁡x=cos⁡xsin⁡x+sin⁡xcos⁡x=cos⁡2x+sin⁡2xsin⁡xcos⁡x=1sin⁡xcos⁡x\cot x + \tan x = \frac{\cos x}{\sin x} + \frac{\sin x}{\cos x} = \frac{\cos^2 x + \sin^2 x}{\sin x \cos x} = \frac{1}{\sin x \cos x}. Also, from the double angle formula for sine, sin⁡(2x)=2sin⁡xcos⁡x\sin(2x) = 2 \sin x \cos x, so sin⁡xcos⁡x=12sin⁡(2x)\sin x \cos x = \frac{1}{2}\sin(2x). Therefore, cot⁡x+tan⁡x=112sin⁡(2x)=2sin⁡(2x)\cot x + \tan x = \frac{1}{\frac{1}{2}\sin(2x)} = \frac{2}{\sin(2x)}.

Equating the two expressions for cot⁡x+tan⁡x\cot x + \tan x: 2sin⁡(2x)=π2+nπ=π(1+2n)2=π(2n+1)2\frac{2}{\sin(2x)} = \frac{\pi}{2} + n\pi = \frac{\pi(1+2n)}{2} = \frac{\pi(2n+1)}{2}

Solving for sin⁡(2x)\sin(2x): sin⁡(2x)=2π(2n+1)2=4π(2n+1)\sin(2x) = \frac{2}{\frac{\pi(2n+1)}{2}} = \frac{4}{\pi(2n+1)}