Question

If $i = \sqrt{-1}$ and $\left(1+\frac{1}{1^2}\right)\left(1+\frac{1}{(1+i)^2}\right)\left(1+\frac{1}{(1+2i)^2}\right)...\left(1+\frac{1}{(1+(n-1)i)^2}\right)=\frac{10+8i}{1+8i}$, then n is equal to

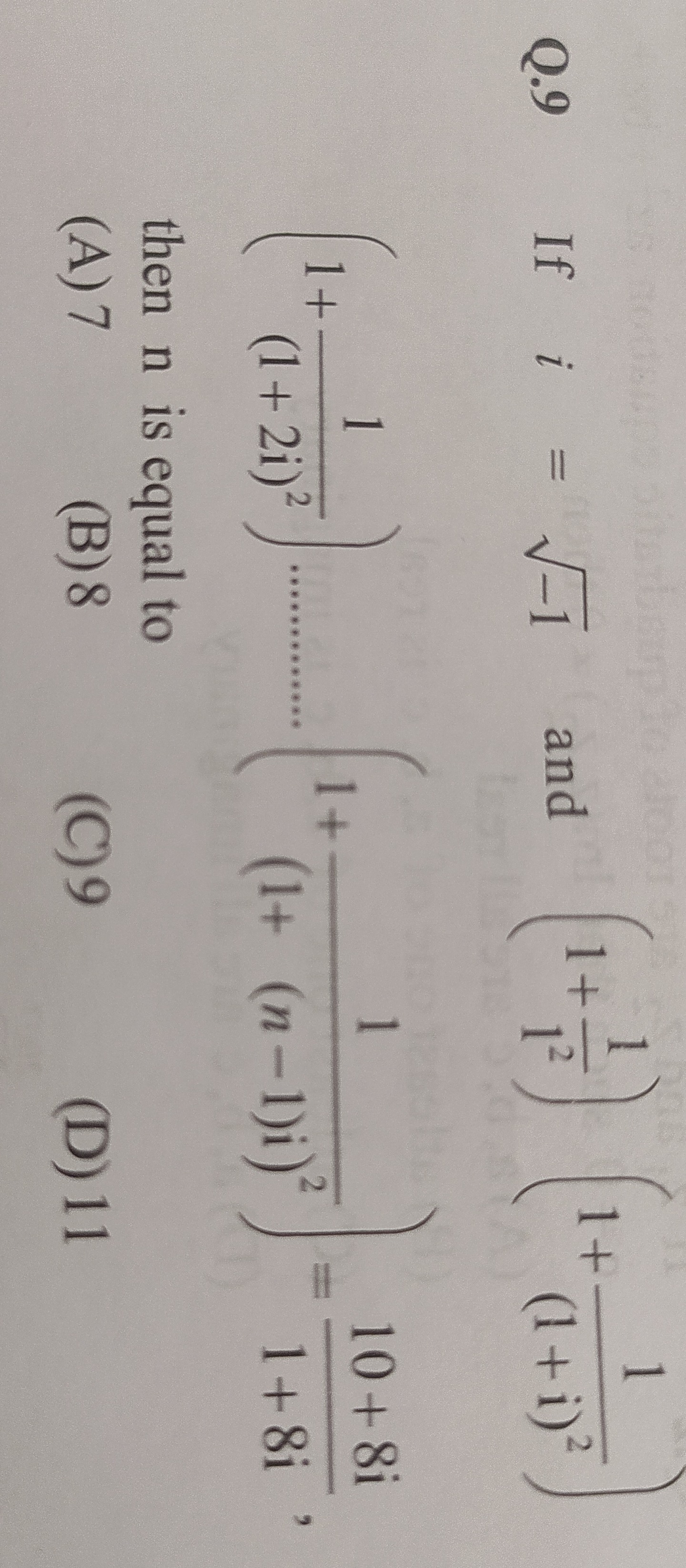
• A. 7
• B. 8
• C. 9
• D. 11

Answer 1

Answer: (C)

9

Answer 2

We are given

$$P=\prod_{k=0}^{n-1}\left(1+\frac{1}{(1+ki)^2}\right)=\frac{10+8i}{1+8i}.$$

Write each term as

$$1+\frac{1}{(1+ki)^2}=\frac{(1+ki)^2+1}{(1+ki)^2}.$$

Notice that

$$(1+ki)^2+1=(1+ki+i)(1+ki-i),$$

so

$$P=\frac{\prod_{k=0}^{n-1}[1+ki+i]\;\prod_{k=0}^{n-1}[1+ki-i]}{\prod_{k=0}^{n-1}(1+ki)^2}.$$

Define

$$A=\prod_{k=0}^{n-1}\frac{1+ki+i}{1+ki} \quad \text{and} \quad B=\prod_{k=0}^{n-1}\frac{1+ki-i}{1+ki}.$$

Notice for $A$ the product telescopes:

$$A=\frac{1+1\cdot i}{1+0\cdot i}\cdot\frac{1+2i}{1+i}\cdots\frac{1+ni}{1+(n-1)i}=\frac{1+ni}{1}.$$

Similarly, for $B$ we have:

$$B=\frac{1-i}{1}\cdot\frac{1}{1+i}\cdot\frac{1+i}{1+2i}\cdots\frac{1+(n-2)i}{1+(n-1)i}=\frac{1-i}{1+(n-1)i}.$$

Thus,

$$P=A\cdot B=\frac{(1+ni)(1-i)}{1+(n-1)i}.$$

Now compute the numerator:

$$(1+ni)(1-i)=1\cdot(1-i)+ni\cdot(1-i)=1-i+ni-n i^2=(1+n)+(n-1)i.$$

Thus,

$$P=\frac{(1+n)+(n-1)i}{1+(n-1)i}.$$

Equate this to the given value:

$$\frac{(1+n)+(n-1)i}{1+(n-1)i}=\frac{10+8i}{1+8i}.$$

Cross-multiply:

$$[(1+n)+(n-1)i](1+8i)=(10+8i)(1+(n-1)i).$$

Expanding the LHS:

$$[(1+n)+(n-1)i](1+8i) = (1+n)(1+8i) + (n-1)i(1+8i).$$ $$= (1+n)+8(1+n)i +(n-1)i+8(n-1)i^2.$$

Since $i^2=-1$,

$$= (1+n) - 8(n-1) +\Big[8(1+n)+(n-1)\Big]i.$$

Simplify:

$$\text{Real part}: 1+n-8n+8=9-7n,$$ $$\text{Imaginary part}: 8+8n+n-1=7+9n.$$

Thus, LHS becomes:

$$(9-7n)+(7+9n)i.$$

Expanding the RHS:

$$(10+8i)(1+(n-1)i)=10\cdot(1+(n-1)i)+8i\cdot(1+(n-1)i).$$ $$=10+10(n-1)i+8i+8(n-1)i^2.$$ $$=10-8(n-1)+(10(n-1)+8)i \quad (\text{since } i^2=-1).$$

Simplify:

$$\text{Real part}: 10-8n+8=18-8n,$$ $$\text{Imaginary part}: 10n-10+8=10n-2.$$

Thus, RHS is:

$$(18-8n)+(10n-2)i.$$

Equate real and imaginary parts:

Real part:

$$9-7n=18-8n \quad\Rightarrow\quad 9-7n+8n=18 \quad\Rightarrow\quad n=9.$$

Imaginary part:

$$7+9n=10n-2 \quad\Rightarrow\quad 7+9(9)=10(9)-2 \quad\Rightarrow\quad 7+81=90-2,\quad 88=88.$$

Thus, $n=9$.