Question
Question: If galvanometer shows null deflection in the give figure then the value of Y is...
If galvanometer shows null deflection in the give figure then the value of Y is
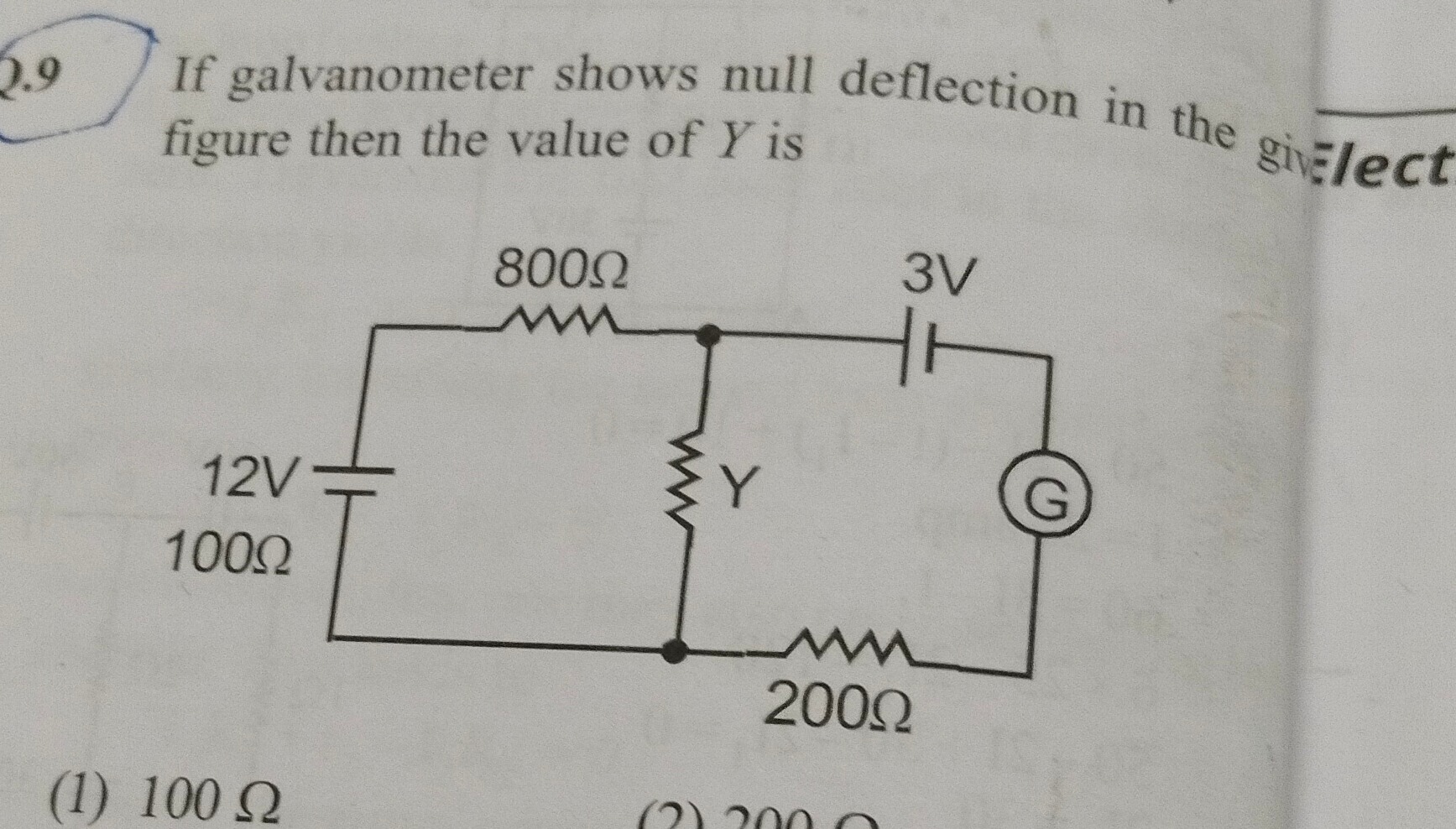
100 Ω
200 Ω
Solution
The circuit is a Wheatstone bridge with two voltage sources. For the galvanometer to show null deflection, the potential difference across its terminals must be zero. Assuming the galvanometer is connected between the junction of the 800 Ω resistor and Y (let's call this point B), and the junction of Y and the 200 Ω resistor (let's call this point C), then VB=VC for null deflection.
Let's analyze the potentials. Let the bottom wire be at 0V. The top left node (connected to the 12V battery) is at 12V. The potential at point B can be found using potential division if we consider the left branch of the circuit: VB=12V×800Ω+YY (This assumes the 12V is applied across 800 Ω and Y in series, which is incorrect due to the other branch).
A more accurate approach involves nodal analysis or superposition. However, a common pattern in such bridge circuits with two voltage sources is that for balance, the voltage drops across corresponding branches are equal.
Let's consider the potential difference across the galvanometer. For null deflection, the potential at point B must be equal to the potential at point C. VB=VC
Let's apply Kirchhoff's voltage law around the loops. Consider the left loop: 12V−I1×800Ω−I2×Y=0 Consider the right loop: VB−VC=3V (given by the battery). If galvanometer shows null deflection, VB=VC. This implies 3V=0, which is a contradiction if the galvanometer is directly between B and C.
Let's assume the galvanometer is connected between the junction of 800 Ω and Y, and the junction of Y and 200 Ω. For null deflection, VB=VC.
Let's use nodal analysis with the bottom wire as reference (0V). Let VA be the potential at the top left node. VA=12V. Let VB be the potential at the junction of 800 Ω and Y. Let VC be the potential at the junction of Y and 200 Ω.
Current through 800 Ω resistor (from A to B): IAB=800VA−VB=80012−VB. Current through Y resistor (from B to C): IBC=YVB−VC. Current through 200 Ω resistor (from C to D, where D is at 0V): ICD=200VC−0=200VC.
The 3V battery is connected between B and C. Let's assume the positive terminal is at B. So, VB−VC=3V. For null deflection, the current through the galvanometer is zero. If the galvanometer is connected between B and C, and it shows null deflection, it implies VB=VC. This contradicts VB−VC=3V.
The problem statement implies a balanced condition. In a typical Wheatstone bridge, balance occurs when R2R1=R4R3. However, this circuit has voltage sources in the arms.
Let's consider the case where the 3V battery is in series with the galvanometer between points B and C. For null deflection, the net potential difference across the galvanometer is zero. This means that the voltage drop from B to C through the galvanometer is zero.
A common interpretation for such circuits with two voltage sources in a bridge configuration is that the ratio of resistances in the arms balanced by the voltage sources should be equal.
Consider the left arm with the 12V source and the 800 Ω resistor. Consider the right arm with the 200 Ω resistor and the bottom wire (0V).
If we consider the voltage division effect: Potential at B due to the 12V source: VB1=12×800+YY Potential at C due to the 12V source: VC1=12×Y+200200 (This is not correct as Y and 200 are not in series with 12V).
Let's assume the question implies a condition where the voltage drop across the 800 Ω resistor is proportional to the voltage drop across the 200 Ω resistor, and similarly for Y and the 3V battery.
A key insight for bridge circuits with voltage sources is that for balance, the voltage difference between the two points connected by the galvanometer is zero.
Let's re-evaluate the setup. The galvanometer is connected between the junction of 800 Ω and Y, and the junction of Y and 200 Ω. Let's call these points B and C. So, for null deflection, VB=VC.
Let's consider the potential at point B. It is influenced by the 12V source and the 800 Ω resistor. Let's consider the potential at point C. It is influenced by the 3V source and the 200 Ω resistor.
If we consider the circuit as a bridge, the condition for balance is often related to the ratio of resistances. However, we have two voltage sources.
Let's consider the problem as a superposition of two circuits: one with the 12V source and one with the 3V source.
Circuit 1: Only 12V source active. Let the bottom wire be 0V. Then the top left node is 12V. The potential at B is VB1=12×800+YY (assuming Y is in series with 800, which is not entirely correct due to the parallel branch). The potential at C is VC1=12×800+200200 if Y was not there.
Let's use a more standard interpretation of a bridge with two voltage sources. The condition for null deflection is that the ratio of resistances in the arms is equal, considering the voltage sources.
Consider the left branch: 12V source and 800 Ω. Consider the right branch: 3V source and Y.
If we consider the voltage division: Potential at B, relative to the bottom wire: VB=12−Ileft×800. Potential at C, relative to the bottom wire: VC=VB−3 (if positive at B).
Let's assume the standard Wheatstone bridge condition applies in a modified form. For a bridge circuit with resistances R1,R2,R3,R4 and a galvanometer across the diagonal, balance is R2R1=R4R3.
In this circuit, we have two voltage sources. Let's assume the galvanometer is connected between the junction of 800 Ω and Y, and the junction of Y and 200 Ω. Let the top left node be A, the junction between 800 Ω and Y be B, the junction between Y and 200 Ω be C, and the bottom wire be D. VA−VD=12V. VB−VC=3V. For null deflection, VB=VC. This is a contradiction.
There must be a misunderstanding of the circuit diagram or the galvanometer's placement. Assuming the galvanometer is measuring the potential difference between the junction of 800 Ω and Y, and the junction of Y and 200 Ω.
Let's consider the circuit as a generalized Wheatstone bridge with two voltage sources. The condition for null deflection is that the ratio of voltage drops across corresponding branches is equal.
Consider the left side: 12V battery and 800 Ω. Consider the right side: 3V battery and Y.
If we consider the voltage division, for balance: Y800Ω=3V12V is incorrect.
Let's consider the potential difference between points B and C. If the galvanometer is connected between the junction of 800 Ω and Y, and the junction of Y and 200 Ω. Let Vbottom=0. Vtop_left=12V.
Using nodal analysis: At node B: 800VB−12+YVB−VC+IG=0 At node C: YVC−VB−200VC−0−IG=0 Also, VB−VC=3V. For null deflection, IG=0.
So, at node B: 800VB−12+YVB−VC=0. At node C: YVC−VB−200VC=0.
Substitute VB−VC=3V into the first equation: 800VB−12+Y3=0⟹VB−12=−Y3×800⟹VB=12−Y2400.
Substitute VC−VB=−3V into the second equation: Y−3−200VC=0⟹−Y3=200VC⟹VC=−Y600.
Now, use VB−VC=3: (12−Y2400)−(−Y600)=3 12−Y2400+Y600=3 12−Y1800=3 9=Y1800 Y=91800=200Ω.
Therefore, the value of Y is 200 Ω.
