Question

If $D = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}$ and corresponding cofactors of elements be written as $c_{11}, c_{12}, c_{21}$ and $c_{22}$, then the value of $a_{11}c_{21} + a_{12}c_{22} + a_{21}c_{11} + a_{22}c_{12}$ is equal to

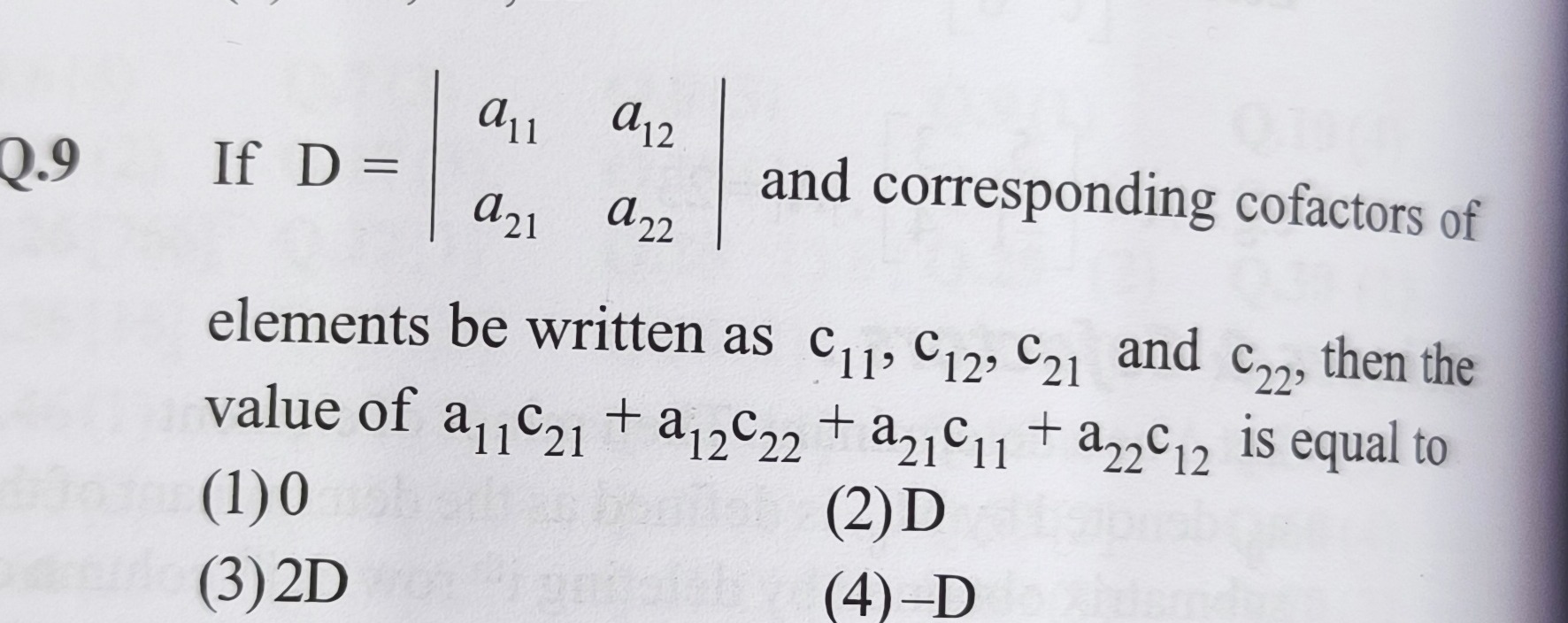
• A. 0
• B. D
• C. 2D
• D. -D

Answer 1

Answer: (A)

0

Answer 2

For the $2 \times 2$ matrix

$$A=\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix},$$

the determinant is

$$D = a_{11}a_{22} - a_{12}a_{21}.$$

The cofactors are:

$$c_{11} = a_{22}, \quad c_{12} = -a_{21}, \quad c_{21} = -a_{12}, \quad c_{22} = a_{11}.$$

Now, calculate the expression:

$$a_{11}c_{21} + a_{12}c_{22} + a_{21}c_{11} + a_{22}c_{12}$$

Substituting the cofactors:

$$= a_{11}(-a_{12}) + a_{12}(a_{11}) + a_{21}(a_{22}) + a_{22}(-a_{21})$$ $$= -a_{11}a_{12} + a_{11}a_{12} + a_{21}a_{22} - a_{21}a_{22} = 0.$$