Question

If D = $\begin{vmatrix} a^2+1 & ab & ac \\ ba & b^2+1 & bc \\ ca & cb & c^2+1 \end{vmatrix}$ then D =

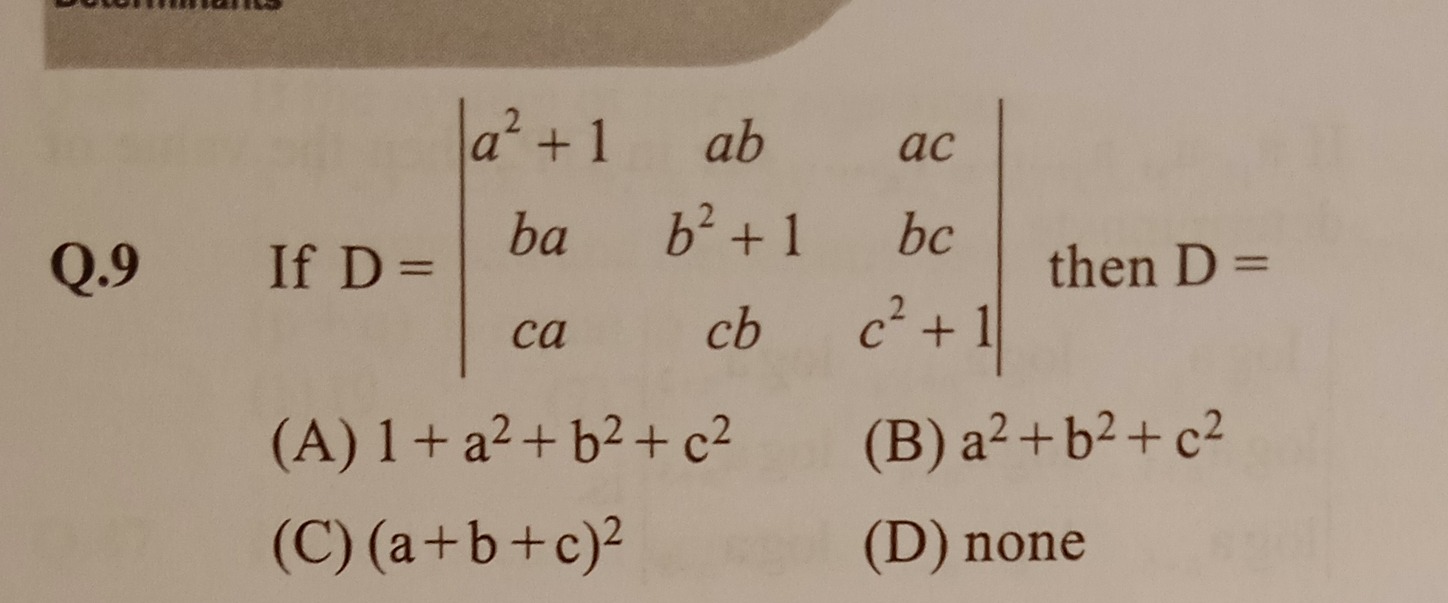
• A. $1+a^2+b^2+c^2$
• B. $a^2+b^2+c^2$
• C. $(a+b+c)^2$
• D. none

Answer 1

Answer: (A)

$1+a^2+b^2+c^2$

Answer 2

The determinant is evaluated by first transforming the matrix using row and column operations. Multiply rows by $a, b, c$ and divide by $abc$. Then take out $a, b, c$ from columns, which cancels $abc$. This results in a simpler matrix. Then apply $R_1 \to R_1 + R_2 + R_3$ and factor out the common term from $R_1$. Finally, perform column operations to create zeros, resulting in a triangular matrix whose determinant is easily calculated as the product of diagonal elements.