Question
Question: Which term of sequence $\sqrt{3}, 3, 3\sqrt{3}, \dots \dots \dots \dots \dots \dots \dots$ is 243?...
Which term of sequence 3,3,33,………………… is 243?
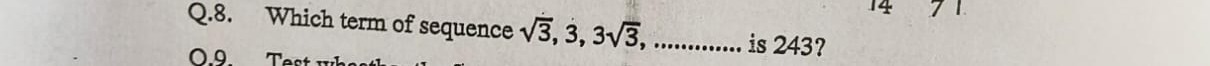
Answer
The 10th term is 243.
Explanation
Solution
Given the sequence:
3,3,33,…This is a geometric progression.
- First term, a=3
- Common ratio, r=33=3
The nth term is:
an=a⋅rn−1=3⋅(3)n−1=(3)nWe require:
(3)n=243Expressing in terms of powers of 3:
(3)n=32nAnd since 243=35, we equate:
32n=35⟹2n=5⟹n=10