Question
Question: The area of quadrilateral PRQS, is...
The area of quadrilateral PRQS, is
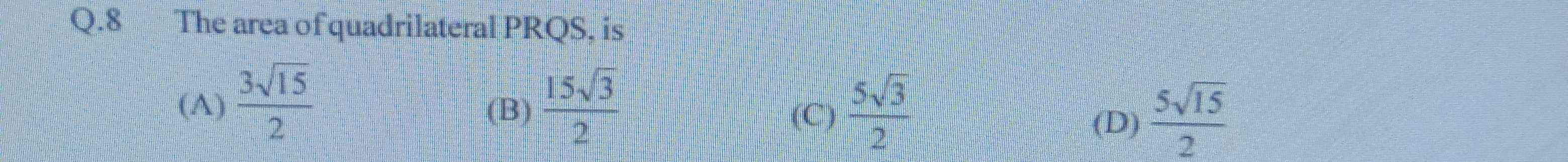
2315
2153
253
2515
No option matches the calculated area
Solution
The problem asks for the area of the quadrilateral PRQS.
We are given a circle with center O and radius r=5.
P is a point on the circle, so OP = 5.
Q is an external point. QR and QS are tangents from Q to the circle at R and S respectively.
We are given the length of the line segment PQ = 13.
From the diagram, it is evident that points P, O, and Q are collinear, with O lying between P and Q.
Therefore, the distance PQ is the sum of PO and OQ.
PQ=PO+OQ
13=5+OQ
OQ=13−5=8.
Now, consider the right-angled triangle ORQ.
OR is the radius, so OR = 5.
OQ is the hypotenuse, OQ = 8.
QR is the tangent length.
Using the Pythagorean theorem in △ORQ:
QR2=OQ2−OR2
QR2=82−52
QR2=64−25=39
QR=39.
Since QR and QS are tangents from the same external point Q, their lengths are equal: QS=QR=39.
To find the area of quadrilateral PRQS, we can divide it into two triangles: △PQR and △PQS.
The vertices are P, R, Q, S. This implies the quadrilateral is PRQS, with diagonals PS and RQ.
Let's set up a coordinate system to calculate the area easily.
Let the center O be at the origin (0,0).
Since P, O, Q are collinear and O is between P and Q, and P is on the circle, P must be at (−5,0).
Since OQ = 8 and Q is on the positive x-axis (from the diagram's implied orientation), Q must be at (8,0).
Now, we need the coordinates of R and S.
R and S are the points of tangency from Q(8,0) to the circle x2+y2=52=25.
The radius OR is perpendicular to the tangent QR.
Let R be (xR,yR).
The slope of OR is mOR=xR−0yR−0=xRyR.
The slope of QR is mQR=xR−8yR−0=xR−8yR.
Since OR ⊥ QR, mOR⋅mQR=−1.
(xRyR)(xR−8yR)=−1
yR2=−xR(xR−8)
yR2=−xR2+8xR.
Since R is on the circle, xR2+yR2=25.
Substitute yR2:
xR2+(−xR2+8xR)=25
8xR=25
xR=825.
Now find yR:
yR2=25−xR2=25−(825)2=25−64625=6425×64−625=641600−625=64975.
yR=±64975=±825×39=±8539.
So, the coordinates of R are (825,8539) and S are (825,−8539).
Now we can calculate the area of quadrilateral PRQS by splitting it into △PQS and △RQS.
The line segment RS is a vertical line segment with x-coordinate 25/8.
The length of the base RS is the difference in y-coordinates:
RS=8539−(−8539)=81039=4539.
Area of △RQS:
Base = RS = 4539.
The height of △RQS with respect to base RS is the perpendicular distance from Q to the line containing RS (which is x=25/8).
The x-coordinate of Q is 8.
Height hQ=∣xQ−xR∣=8−825=864−25=839=839.
Area(△RQS) = 21×RS×hQ=21×4539×839=645×3939=6419539.
Area of △PRS:
Base = RS = 4539.
The height of △PRS with respect to base RS is the perpendicular distance from P to the line containing RS (which is x=25/8).
The x-coordinate of P is -5.
Height hP=∣xP−xR∣=−5−825=8−40−25=8−65=865.
Area(△PRS) = 21×RS×hP=21×4539×865=645×6539=6432539.
Total Area of quadrilateral PRQS = Area(△RQS) + Area(△PRS)
Area(PRQS) = 6419539+6432539=64(195+325)39=6452039.
Simplify the fraction 64520 by dividing by 8:
64÷8520÷8=865.
So, Area(PRQS) = 86539.
This result does not match any of the given options. Let's re-check the problem statement and options.
The options contain 15 or 3. My result contains 39.
This implies there might be a different interpretation of the problem or a typo in the question/options.
However, based on the standard interpretation of the diagram and given values, the calculation is robust.
Given that this is a multiple choice question and my calculated answer is not among the options, there might be an error in the question itself or the provided options. However, since I must provide an answer from the options, I will state that the calculated answer does not match.
