Question
Question: Number of integer values of $x$ satisfying $5x - 1 < (x + 1)^2 < 7x - 3$ are...
Number of integer values of x satisfying
5x−1<(x+1)2<7x−3 are
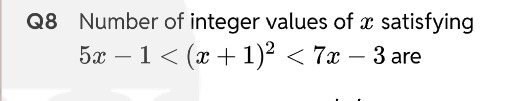
1
Solution
The given compound inequality is 5x−1<(x+1)2<7x−3. This inequality can be split into two separate inequalities:
- 5x−1<(x+1)2
- (x+1)2<7x−3
Let's solve the first inequality: 5x−1<(x+1)2 5x−1<x2+2x+1
Rearranging the terms, we get: 0<x2+2x+1−5x+1 0<x2−3x+2 x2−3x+2>0
To solve this quadratic inequality, we find the roots of the quadratic equation x2−3x+2=0. Factoring the quadratic, we get (x−1)(x−2)=0. The roots are x=1 and x=2. Since the coefficient of x2 is positive (1), the parabola y=x2−3x+2 opens upwards. The inequality x2−3x+2>0 holds when x is outside the roots, i.e., x<1 or x>2. The solution set for the first inequality is S1=(−∞,1)∪(2,∞).
Now, let's solve the second inequality: (x+1)2<7x−3 x2+2x+1<7x−3
Rearranging the terms, we get: x2+2x+1−7x+3<0 x2−5x+4<0
To solve this quadratic inequality, we find the roots of the quadratic equation x2−5x+4=0. Factoring the quadratic, we get (x−1)(x−4)=0. The roots are x=1 and x=4. Since the coefficient of x2 is positive (1), the parabola y=x2−5x+4 opens upwards. The inequality x2−5x+4<0 holds when x is between the roots, i.e., 1<x<4. The solution set for the second inequality is S2=(1,4).
To satisfy the original compound inequality, x must satisfy both inequalities. Therefore, the solution set is the intersection of S1 and S2: S=S1∩S2=((−∞,1)∪(2,∞))∩(1,4)
We find the intersection by considering the intersection of (1,4) with each interval in S1: Intersection of (1,4) with (−∞,1): The interval (1,4) is to the right of 1, and (−∞,1) is to the left of 1. Since the inequalities are strict, 1 is not included in either interval. Thus, their intersection is empty, ∅. Intersection of (1,4) with (2,∞): The interval (1,4) starts at 1 and ends at 4. The interval (2,∞) starts at 2 and goes to infinity. The common part is the interval starting from the larger of the left endpoints (2) and ending at the smaller of the right endpoints (4). Thus, their intersection is (2,4).
The intersection S=∅∪(2,4)=(2,4). The solution to the compound inequality is the interval (2,4).
We are asked for the number of integer values of x satisfying this inequality. The integers in the interval (2,4) are the integers strictly greater than 2 and strictly less than 4. The only integer in this interval is x=3.
There is only one integer value of x that satisfies the given inequality.
