Solveeit Logo
Login

Question

Question: If angle between two vectors $\overline{a}$ and $\overline{b}$ is $\pi/6$, $|\overline{a}| = 1$, $|\...

If angle between two vectors a‾\overline{a} and b‾\overline{b} is π/6\pi/6, ∣a‾∣=1|\overline{a}| = 1, ∣b‾∣=3|\overline{b}| = \sqrt{3} such that vectors 3(a‾×b‾)3(\overline{a} \times \overline{b}) and 2(b‾−(a‾.b‾)a‾)2(\overline{b} - (\overline{a}.\overline{b})\overline{a}) represent two sides of a triangle then its area in square units

A

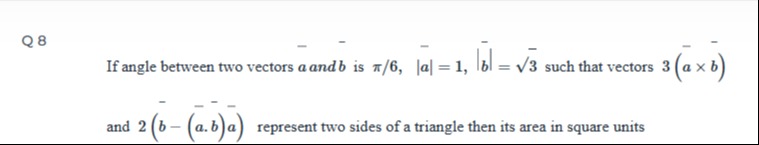
9/4

B

3/4

C

9/2

D

3/2

Answer

9/4

Explanation

Solution

The area of a triangle with adjacent sides represented by vectors p‾\overline{p} and q‾\overline{q} is given by 12∣p‾×q‾∣\frac{1}{2} |\overline{p} \times \overline{q}|.

Given vectors a‾\overline{a} and b‾\overline{b} with: Angle θ=π/6\theta = \pi/6 ∣a‾∣=1|\overline{a}| = 1 ∣b‾∣=3|\overline{b}| = \sqrt{3}

First, calculate the scalar product and the magnitude of the cross product of a‾\overline{a} and b‾\overline{b}: a‾⋅b‾=∣a‾∣∣b‾∣cos⁡θ=(1)(3)cos⁡(π/6)=3(32)=32\overline{a} \cdot \overline{b} = |\overline{a}| |\overline{b}| \cos \theta = (1)(\sqrt{3}) \cos(\pi/6) = \sqrt{3} \left(\frac{\sqrt{3}}{2}\right) = \frac{3}{2}. ∣a‾×b‾∣=∣a‾∣∣b‾∣sin⁡θ=(1)(3)sin⁡(π/6)=3(12)=32|\overline{a} \times \overline{b}| = |\overline{a}| |\overline{b}| \sin \theta = (1)(\sqrt{3}) \sin(\pi/6) = \sqrt{3} \left(\frac{1}{2}\right) = \frac{\sqrt{3}}{2}.

Let the two sides of the triangle be: p‾=3(a‾×b‾)\overline{p} = 3(\overline{a} \times \overline{b}) q‾=2(b‾−(a‾⋅b‾)a‾)\overline{q} = 2(\overline{b} - (\overline{a} \cdot \overline{b})\overline{a})

We need to calculate p‾×q‾\overline{p} \times \overline{q}: p‾×q‾=[3(a‾×b‾)]×[2(b‾−(a‾⋅b‾)a‾)]\overline{p} \times \overline{q} = [3(\overline{a} \times \overline{b})] \times [2(\overline{b} - (\overline{a} \cdot \overline{b})\overline{a})] p‾×q‾=6(a‾×b‾)×(b‾−32a‾)\overline{p} \times \overline{q} = 6 (\overline{a} \times \overline{b}) \times (\overline{b} - \frac{3}{2}\overline{a}) Using the distributive property of the cross product: p‾×q‾=6[(a‾×b‾)×b‾−(a‾×b‾)×(32a‾)]\overline{p} \times \overline{q} = 6 [(\overline{a} \times \overline{b}) \times \overline{b} - (\overline{a} \times \overline{b}) \times (\frac{3}{2}\overline{a})]

Using the vector triple product identity, u‾×(v‾×w‾)=(u‾⋅w‾)v‾−(u‾⋅v‾)w‾\overline{u} \times (\overline{v} \times \overline{w}) = (\overline{u} \cdot \overline{w})\overline{v} - (\overline{u} \cdot \overline{v})\overline{w}: (a‾×b‾)×b‾=(a‾⋅b‾)b‾−(b‾⋅b‾)a‾=32b‾−3a‾(\overline{a} \times \overline{b}) \times \overline{b} = (\overline{a} \cdot \overline{b})\overline{b} - (\overline{b} \cdot \overline{b})\overline{a} = \frac{3}{2}\overline{b} - 3\overline{a}. (a‾×b‾)×a‾=(a‾⋅a‾)b‾−(a‾⋅b‾)a‾=(1)b‾−32a‾=b‾−32a‾(\overline{a} \times \overline{b}) \times \overline{a} = (\overline{a} \cdot \overline{a})\overline{b} - (\overline{a} \cdot \overline{b})\overline{a} = (1)\overline{b} - \frac{3}{2}\overline{a} = \overline{b} - \frac{3}{2}\overline{a}.

Substitute these back into the expression for p‾×q‾\overline{p} \times \overline{q}: p‾×q‾=6[(32b‾−3a‾)−32(b‾−32a‾)]\overline{p} \times \overline{q} = 6 \left[ \left(\frac{3}{2}\overline{b} - 3\overline{a}\right) - \frac{3}{2}\left(\overline{b} - \frac{3}{2}\overline{a}\right) \right] p‾×q‾=6[32b‾−3a‾−32b‾+94a‾]\overline{p} \times \overline{q} = 6 \left[ \frac{3}{2}\overline{b} - 3\overline{a} - \frac{3}{2}\overline{b} + \frac{9}{4}\overline{a} \right] p‾×q‾=6[(−3+94)a‾]=6[−34a‾]=−92a‾\overline{p} \times \overline{q} = 6 \left[ \left(-3 + \frac{9}{4}\right)\overline{a} \right] = 6 \left[ -\frac{3}{4}\overline{a} \right] = -\frac{9}{2}\overline{a}.

The area of the triangle is 12∣p‾×q‾∣\frac{1}{2} |\overline{p} \times \overline{q}|: Area =12∣−92a‾∣=12(92)∣a‾∣=12×92×1=94= \frac{1}{2} \left|-\frac{9}{2}\overline{a}\right| = \frac{1}{2} \left(\frac{9}{2}\right) |\overline{a}| = \frac{1}{2} \times \frac{9}{2} \times 1 = \frac{9}{4}.