Question

A certain radioactive nuclide of mass number $m_x$ disintegrates, with the emission of an electron and $\gamma$ radiation only, to give second nuclied of mass number $m_y$. Which one of the following equation correctly relates $m_x$ and $m_y$?

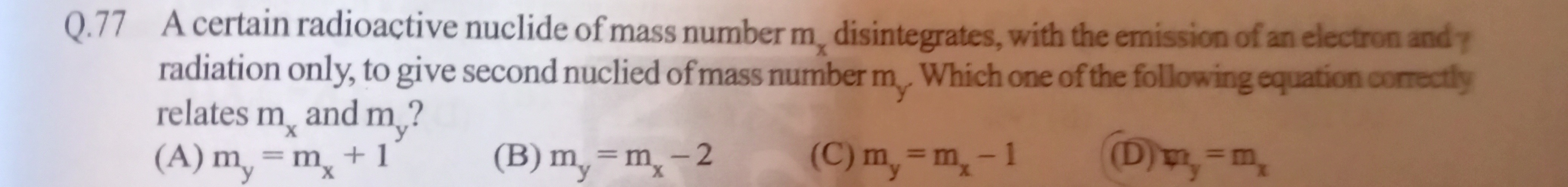
• A. m_y = m_x + 1
• B. m_y = m_x - 2
• C. m_y = m_x - 1
• D. m_y = m_x

Answer 1

Answer: (D)

m_y = m_x

Answer 2

The radioactive decay described involves the emission of an electron, which is characteristic of beta-minus ($\beta^-$) decay. In $\beta^-$ decay, a neutron within the nucleus transforms into a proton, an electron (emitted as a beta particle), and an antineutrino. Gamma ($\gamma$) radiation is electromagnetic radiation and does not affect the mass number or atomic number of the nucleus.

The transformation of a neutron into a proton can be represented as: $n \rightarrow p + e^- + \bar{\nu}_e$

Let the initial nuclide be denoted by $X$ with mass number $m_x$ and atomic number $Z_x$. Let the resulting nuclide be $Y$ with mass number $m_y$ and atomic number $Z_y$. The decay process can be written as: $_ {Z_x}^{m_x} X \rightarrow _ {Z_y}^{m_y} Y + e^- + \gamma$

In this process, the number of nucleons (protons + neutrons) remains constant. A neutron is replaced by a proton, but the total count of these particles stays the same. Therefore, the mass number ($m$) of the nuclide does not change.

Thus, the mass number of the initial nuclide ($m_x$) is equal to the mass number of the final nuclide ($m_y$). $m_y = m_x$