Question
Question: In the expansion of $(1+x)^n(1+y)^n(1+z)^n$, the sum of the co-efficients of the terms of degree 'r'...
In the expansion of (1+x)n(1+y)n(1+z)n, the sum of the co-efficients of the terms of degree 'r' is
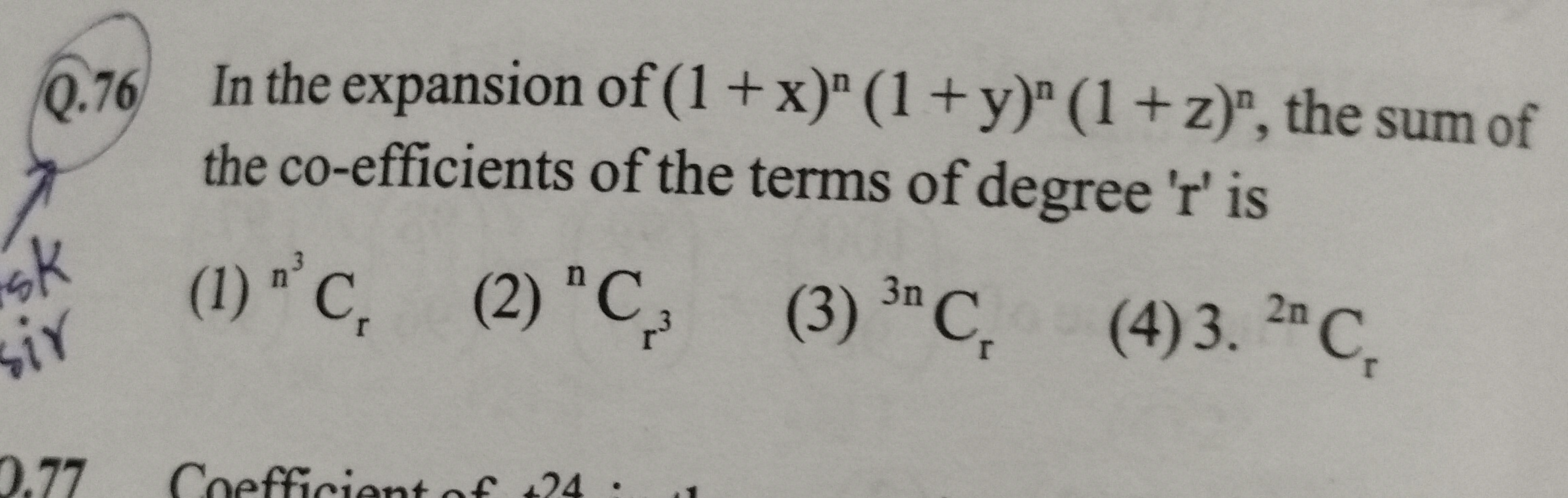
A
nCr
B
nCr3
C
3nCr
D
3.2nCr
Answer
3nCr
Explanation
Solution
The sum of coefficients of terms of degree 'r' in a polynomial P(x1,x2,…,xm) is equal to the coefficient of tr in the polynomial P(t,t,…,t).
Given the expression P(x,y,z)=(1+x)n(1+y)n(1+z)n. To find the sum of coefficients of terms of degree 'r', we substitute x=t,y=t,z=t: P(t,t,t)=(1+t)n(1+t)n(1+t)n=(1+t)3n.
Now, we expand (1+t)3n using the binomial theorem: (1+t)3n=∑r=03n3nCrtr.
The coefficient of tr in this expansion is 3nCr. Therefore, the sum of the coefficients of the terms of degree 'r' in the original expansion is 3nCr.
