Question
Question: Let $f(\theta) = \sin \theta + \int_{-\pi/2}^{\pi/2} (\sin \theta + t\cos \theta)f(t)dt$. Then the v...
Let f(θ)=sinθ+∫−π/2π/2(sinθ+tcosθ)f(t)dt. Then the value of
∫0π/2f(θ)dθ is ___.
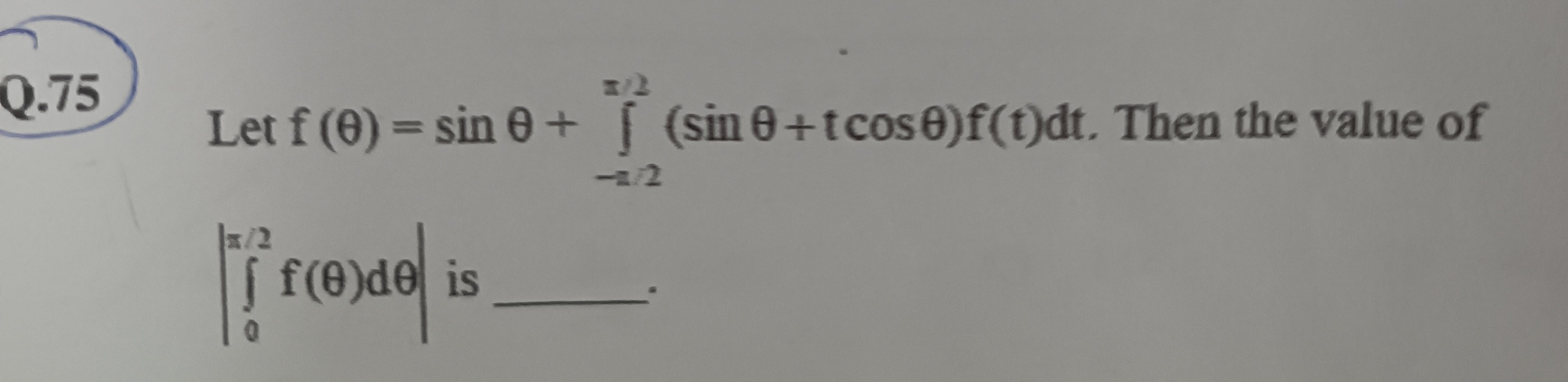
1
Solution
The given integral equation is: f(θ)=sinθ+∫−π/2π/2(sinθ+tcosθ)f(t)dt
First, separate the terms inside the integral: f(θ)=sinθ+∫−π/2π/2sinθf(t)dt+∫−π/2π/2tcosθf(t)dt
Since sinθ and cosθ are constants with respect to the integration variable t, we can take them out of the integral: f(θ)=sinθ+sinθ∫−π/2π/2f(t)dt+cosθ∫−π/2π/2tf(t)dt
Let A=∫−π/2π/2f(t)dt and B=∫−π/2π/2tf(t)dt. Then the expression for f(θ) becomes: f(θ)=sinθ+Asinθ+Bcosθ f(θ)=(1+A)sinθ+Bcosθ
Now, we need to determine the values of A and B.
Substitute f(t) back into the definition of A: A=∫−π/2π/2((1+A)sint+Bcost)dt A=(1+A)∫−π/2π/2sintdt+B∫−π/2π/2costdt
Evaluate the integrals: ∫−π/2π/2sintdt=[−cost]−π/2π/2=−cos(π/2)−(−cos(−π/2))=0−0=0. ∫−π/2π/2costdt=[sint]−π/2π/2=sin(π/2)−sin(−π/2)=1−(−1)=2.
Substitute these values back into the equation for A: A=(1+A)(0)+B(2) A=2B (Equation 1)
Next, substitute f(t) back into the definition of B: B=∫−π/2π/2t((1+A)sint+Bcost)dt B=(1+A)∫−π/2π/2tsintdt+B∫−π/2π/2tcostdt
Evaluate the integrals: For ∫−π/2π/2tsintdt: The integrand g(t)=tsint is an even function (g(−t)=(−t)sin(−t)=tsint=g(t)). So, ∫−π/2π/2tsintdt=2∫0π/2tsintdt. Using integration by parts (∫udv=uv−∫vdu with u=t,dv=sintdt⟹du=dt,v=−cost): ∫0π/2tsintdt=[−tcost−∫(−cost)dt]0π/2=[−tcost+sint]0π/2 =(−π/2cos(π/2)+sin(π/2))−(0cos0+sin0) =(0+1)−(0+0)=1. Thus, ∫−π/2π/2tsintdt=2(1)=2.
For ∫−π/2π/2tcostdt: The integrand h(t)=tcost is an odd function (h(−t)=(−t)cos(−t)=−tcost=−h(t)). For an odd function over a symmetric interval [−a,a], the integral is 0. So, ∫−π/2π/2tcostdt=0.
Substitute these values back into the equation for B: B=(1+A)(2)+B(0) B=2(1+A) (Equation 2)
Now we have a system of two linear equations for A and B:
- A=2B
- B=2(1+A)
Substitute Equation 1 into Equation 2: B=2(1+2B) B=2+4B 3B=−2 B=−2/3
Now find A using Equation 1: A=2B=2(−2/3)=−4/3
So, A=−4/3 and B=−2/3.
Now we can write the explicit form of f(θ): f(θ)=(1+A)sinθ+Bcosθ f(θ)=(1−4/3)sinθ+(−2/3)cosθ f(θ)=(−1/3)sinθ−(2/3)cosθ
Finally, we need to calculate ∫0π/2f(θ)dθ: ∫0π/2f(θ)dθ=∫0π/2(−31sinθ−32cosθ)dθ =−31∫0π/2sinθdθ−32∫0π/2cosθdθ
Evaluate these definite integrals: ∫0π/2sinθdθ=[−cosθ]0π/2=−cos(π/2)−(−cos(0))=0−(−1)=1. ∫0π/2cosθdθ=[sinθ]0π/2=sin(π/2)−sin(0)=1−0=1.
Substitute these values back: ∫0π/2f(θ)dθ=−31(1)−32(1) =−31−32=−33=−1.
The value of ∫0π/2f(θ)dθ is ∣−1∣=1.
The final answer is 1.
