Question

$\begin{vmatrix} 1 & a & a^2-bc \\ 1 & b & b^2-ac \\ 1 & c & c^2 - ab \end{vmatrix} = kabc$, the value of k is:

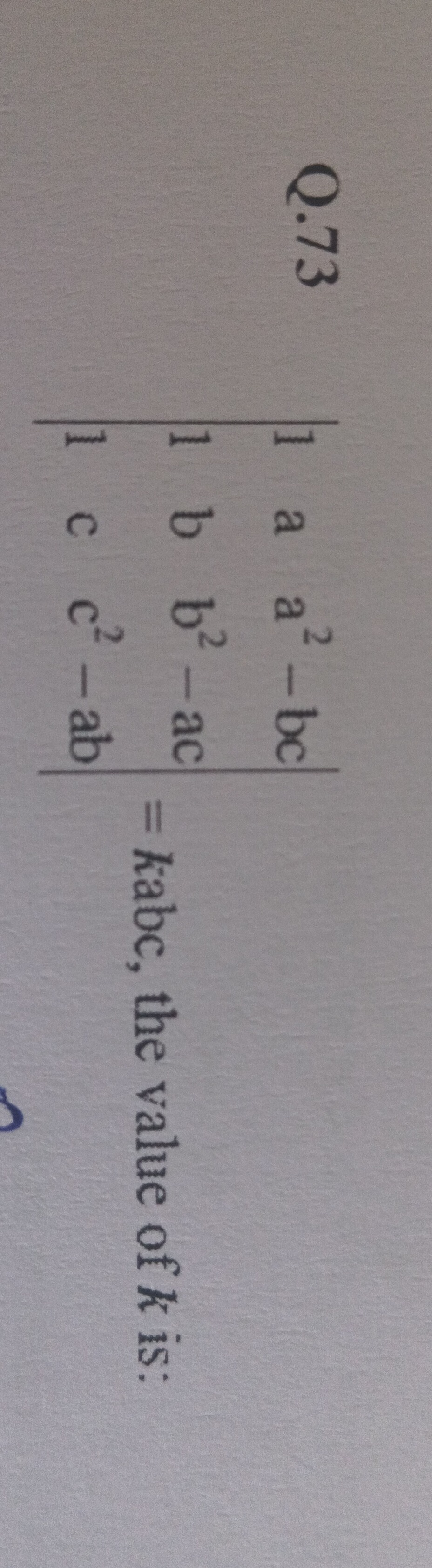
• A. 1
• B. -1
• C. 0
• D. None of these

Answer 1

Answer: (C)

k = 0

Answer 2

We wish to evaluate

$$D=\begin{vmatrix} 1 & a & a^2-bc \\ 1 & b & b^2-ac \\ 1 & c & c^2-ab \end{vmatrix}$$

and write it in the form $k\,a\,b\,c$.

Step 1. Subtract the first row from the second and third rows:

$$\begin{aligned} R_2 &\to R_2 - R_1,\\[1mm] R_3 &\to R_3 - R_1. \end{aligned}$$

After subtraction, the matrix becomes

$$\begin{pmatrix} 1 & a & a^2-bc\\[1mm] 0 & b-a & \bigl(b^2-ac-(a^2-bc)\bigr)\\[1mm] 0 & c-a & \bigl(c^2-ab-(a^2-bc)\bigr) \end{pmatrix}.$$

Step 2. Simplify the third column for $R_2$ and $R_3$.

For $R_2$:

$$\begin{aligned} b^2-ac-(a^2-bc) &= (b^2-a^2) + (bc-ac)\\[1mm] &= (b-a)(b+a) + c(b-a)\\[1mm] &=(b-a)(a+b+c). \end{aligned}$$

Similarly for $R_3$:

$$c^2-ab-(a^2-bc)=(c-a)(a+b+c).$$

Thus the matrix becomes

$$\begin{pmatrix} 1 & a & a^2-bc\\[1mm] 0 & b-a & (b-a)(a+b+c)\\[1mm] 0 & c-a & (c-a)(a+b+c) \end{pmatrix}.$$

Step 3. Now, the determinant simplifies by expanding along the first row:

$$D = 1 \cdot \begin{vmatrix} b-a & (b-a)(a+b+c)\\[1mm] c-a & (c-a)(a+b+c) \end{vmatrix}.$$

Compute the 2×2 determinant:

$$\begin{aligned} \Delta &= (b-a)(c-a)(a+b+c) - (c-a)(b-a)(a+b+c)\\[1mm] &= 0. \end{aligned}$$

Thus, the overall determinant $D = 0$.

Since the problem statement tells us that

$$D = k\,a\,b\,c,$$

we conclude that $k\,a\,b\,c = 0$ for arbitrary $a$, $b$, and $c$. Therefore,

$$k = 0.$$