Question

The value of $\lim_{x\to 0} (\frac{1+2x}{1+3x})^{\frac{1}{x^2}}.e^{\frac{1}{x}}$ is

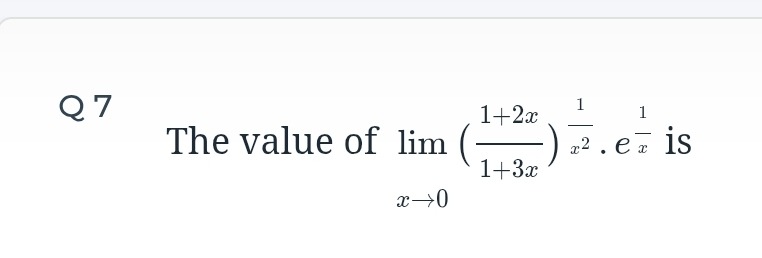
Answer 1

e^{5/2}

Answer 2

Let $L = \lim_{x\to 0} (\frac{1+2x}{1+3x})^{\frac{1}{x^2}}.e^{\frac{1}{x}}$. Taking the natural logarithm of both sides: $\ln L = \lim_{x\to 0} \ln \left[ (\frac{1+2x}{1+3x})^{\frac{1}{x^2}}.e^{\frac{1}{x}} \right]$ $\ln L = \lim_{x\to 0} \left[ \frac{1}{x^2} \ln\left(\frac{1+2x}{1+3x}\right) + \frac{1}{x} \right]$ $\ln L = \lim_{x\to 0} \left[ \frac{\ln(1+2x) - \ln(1+3x) + x}{x^2} \right]$

Using Taylor series expansions around $x=0$: $\ln(1+u) = u - \frac{u^2}{2} + O(u^3)$ $\ln(1+2x) = 2x - \frac{(2x)^2}{2} + O(x^3) = 2x - 2x^2 + O(x^3)$ $\ln(1+3x) = 3x - \frac{(3x)^2}{2} + O(x^3) = 3x - \frac{9x^2}{2} + O(x^3)$

Substitute these into the numerator: Numerator $= (2x - 2x^2) - (3x - \frac{9x^2}{2}) + x + O(x^3)$ Numerator $= (2x - 3x + x) + (-2x^2 + \frac{9x^2}{2}) + O(x^3)$ Numerator $= 0 + \frac{5x^2}{2} + O(x^3)$

So, $\ln L = \lim_{x\to 0} \frac{\frac{5x^2}{2} + O(x^3)}{x^2} = \lim_{x\to 0} (\frac{5}{2} + O(x)) = \frac{5}{2}$. Since $\ln L = \frac{5}{2}$, then $L = e^{5/2}$.