Question
Question: The value of $\int_{0}^{\sin^2 x} \sin^{-1} \sqrt{t}dt + \int_{0}^{\cos^2 x} \cos^{-1} \sqrt{t}dt$...
The value of ∫0sin2xsin−1tdt+∫0cos2xcos−1tdt
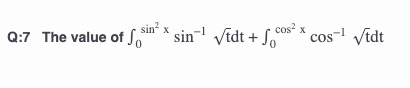
4π
Solution
We need to evaluate
I=∫0sin2xsin−1tdt+∫0cos2xcos−1tdt.Step 1. Differentiate I with respect to x using the Leibniz rule.
For the first integral:
dxd∫0sin2xsin−1tdt=sin−1sin2x⋅dxd(sin2x).Since for x∈[0,π/2], sin2x=sinx and sin−1(sinx)=x, and
dxd(sin2x)=2sinxcosx=sin2x,this term becomes:
xsin2x.For the second integral:
dxd∫0cos2xcos−1tdt=cos−1cos2x⋅dxd(cos2x).Similarly, for x∈[0,π/2] we have cos2x=cosx and cos−1(cosx)=x. Also,
dxd(cos2x)=−2sinxcosx=−sin2x.Thus, the second term is:
x(−sin2x)=−xsin2x.So the derivative of I is
dxdI=xsin2x−xsin2x=0.This shows that I is constant (independent of x).
Step 2. Determine the constant by choosing an easy value of x. Let x=π/2.
Then, sin2(π/2)=1 and cos2(π/2)=0. Therefore,
I=∫01sin−1tdt+∫00cos−1tdt=∫01sin−1tdt.Step 3. Compute J=∫01sin−1tdt.
Let t=u2, so that dt=2udu, and when t=0, u=0; t=1, u=1. Then,
J=∫01sin−1(u)⋅2udu=2∫01usin−1udu.Now, apply integration by parts:
- Let v=sin−1u so that dudv=1−u21.
- Let dw=udu so that w=2u2.
Thus,
∫usin−1udu=2u2sin−1u−∫2u2⋅1−u21du.Multiplying by 2, we have:
2∫01usin−1udu=[ u2sin−1u ]01−∫011−u2u2du.At u=1, sin−11=2π and 12=1. At u=0, the term vanishes. Hence,
2∫01usin−1udu=2π−∫011−u2u2du.Now, evaluate
K=∫011−u2u2du.Substitute u=sinθ so that du=cosθdθ and 1−u2=cosθ. The limits transform to: when u=0, θ=0; when u=1, θ=π/2. Then,
K=∫0π/2cosθsin2θ⋅cosθdθ=∫0π/2sin2θdθ.A standard integral gives:
∫0π/2sin2θdθ=4π.Thus,
2∫01usin−1udu=2π−4π=4π.This means J=4π, and hence
I=4π.