Question

Normals are concurrent drawn at points A, B, and C on the parabola $y^2 = 4x$ at P(h, k). The locus of the point P if the slope of the line joining the feet of two of them is 2, is

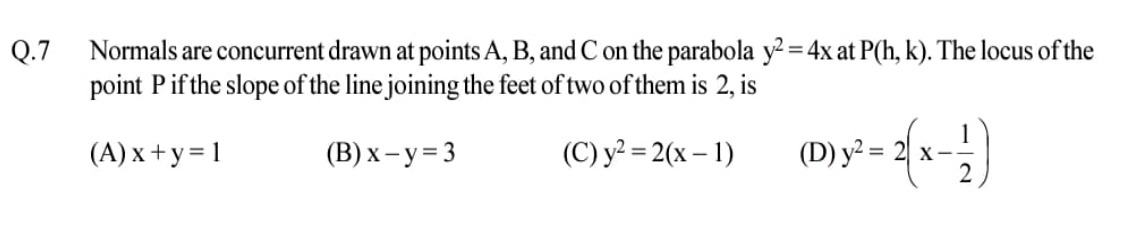
• A. x + y = 1
• B. x - y = 3
• C. $y^2 = 2(x-1)$
• D. $y^2 = 2\left(x-\frac{1}{2}\right)$

Answer 1

Answer: (B)

x - y = 3

Answer 2

The equation of the parabola is $y^2 = 4x$. For a parabola $y^2 = 4ax$, the parameter is $a=1$. The equation of the normal to the parabola $y^2 = 4ax$ at a point $(at^2, 2at)$ is given by $y + tx = 2at + at^3$. Substituting $a=1$, the equation of the normal to $y^2 = 4x$ at $(t^2, 2t)$ is $y + tx = 2t + t^3$.

Let the normals be drawn from the point P(h, k). If the normal passes through P(h, k), then: $k + th = 2t + t^3$ Rearranging this equation, we get a cubic equation in $t$: $t^3 + (2-h)t - k = 0$

Let $t_1, t_2, t_3$ be the roots of this cubic equation. These roots correspond to the parameters of the feet of the three normals (A, B, C) drawn from P(h, k). The coordinates of the feet of the normals are A$(t_1^2, 2t_1)$, B$(t_2^2, 2t_2)$, and C$(t_3^2, 2t_3)$.

From Vieta's formulas for the cubic equation $t^3 + (2-h)t - k = 0$:

1. Sum of the roots: $t_1 + t_2 + t_3 = 0$ (since the coefficient of $t^2$ is 0)
2. Sum of the products of the roots taken two at a time: $t_1t_2 + t_2t_3 + t_3t_1 = 2-h$
3. Product of the roots: $t_1t_2t_3 = -(-k) = k$

We are given that the slope of the line joining the feet of two of them is 2. Let's consider the line joining points A and B. The slope of the line AB is $m_{AB} = \frac{2t_2 - 2t_1}{t_2^2 - t_1^2}$ $m_{AB} = \frac{2(t_2 - t_1)}{(t_2 - t_1)(t_2 + t_1)}$ Assuming $t_1 \neq t_2$ (i.e., the points are distinct), we can cancel $(t_2 - t_1)$: $m_{AB} = \frac{2}{t_1 + t_2}$

We are given that this slope is 2: $\frac{2}{t_1 + t_2} = 2$ This implies $t_1 + t_2 = 1$.

Now, substitute this into the sum of the roots equation from Vieta's formulas: $t_1 + t_2 + t_3 = 0$ $1 + t_3 = 0$ So, $t_3 = -1$.

Since $t_3 = -1$ is a root of the cubic equation $t^3 + (2-h)t - k = 0$, it must satisfy the equation. Substitute $t = -1$ into the equation: $(-1)^3 + (2-h)(-1) - k = 0$ $-1 - (2-h) - k = 0$ $-1 - 2 + h - k = 0$ $h - k - 3 = 0$ $h - k = 3$

The locus of the point P(h, k) is obtained by replacing h with x and k with y. Therefore, the locus of P is $x - y = 3$.