Question

If the sum of the roots of the equation $\lambda x^2 + 2x + 3\lambda = 0$ be equal to their product, then $\lambda$ =

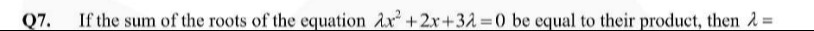
• A. 2/3
• B. -2/3
• C. 3/2
• D. -3/2

Answer 1

Answer: (B)

-2/3

Answer 2

For a quadratic equation $ax^2+bx+c=0$, the sum of roots is $-b/a$ and the product of roots is $c/a$. Given equation: $\lambda x^2 + 2x + 3\lambda = 0$. Here, $a = \lambda$, $b = 2$, $c = 3\lambda$. Sum of roots = $-2/\lambda$. Product of roots = $3\lambda/\lambda$. Given that sum of roots = product of roots: $-2/\lambda = 3\lambda/\lambda$. Assuming $\lambda \neq 0$ (for it to be a quadratic equation), we can cancel $\lambda$ from both sides: $-2 = 3\lambda$. Therefore, $\lambda = -2/3$.