Question
Question: If $\overline a = \hat i + \hat j - 2\hat k$, then the value of $|(\overline a \times \hat i) \times...
If a=i^+j^−2k^, then the value of ∣(a×i^)×j^∣2+∣(a×j^)×i^∣2+∣(a×k^)×i^∣2
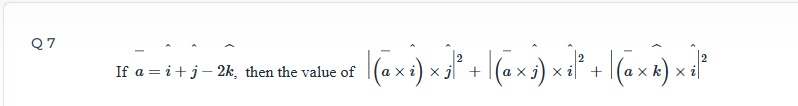
1
2
3
4
3
Solution
We are asked to find the value of ∣(a×i^)×j^∣2+∣(a×j^)×i^∣2+∣(a×k^)×i^∣2, given a=i^+j^−2k^.
We can use the vector triple product identity: (u×v)×w=(u⋅w)v−(v⋅w)u.
Let a=a1i^+a2j^+a3k^. Given a=i^+j^−2k^, we have a1=1, a2=1, and a3=−2.
Let's evaluate each term:
Term 1: ∣(a×i^)×j^∣2 Using the identity with u=a, v=i^, and w=j^: (a×i^)×j^=(a⋅j^)i^−(i^⋅j^)a Since i^⋅j^=0, this simplifies to: (a×i^)×j^=(a⋅j^)i^ The dot product a⋅j^=(a1i^+a2j^+a3k^)⋅j^=a2. So, (a×i^)×j^=a2i^. The magnitude squared is ∣a2i^∣2=a22∣i^∣2=a22(1)2=a22. For a=i^+j^−2k^, a2=1, so the first term is 12=1.
Term 2: ∣(a×j^)×i^∣2 Using the identity with u=a, v=j^, and w=i^: (a×j^)×i^=(a⋅i^)j^−(j^⋅i^)a Since j^⋅i^=0, this simplifies to: (a×j^)×i^=(a⋅i^)j^ The dot product a⋅i^=(a1i^+a2j^+a3k^)⋅i^=a1. So, (a×j^)×i^=a1j^. The magnitude squared is ∣a1j^∣2=a12∣j^∣2=a12(1)2=a12. For a=i^+j^−2k^, a1=1, so the second term is 12=1.
Term 3: ∣(a×k^)×i^∣2 Using the identity with u=a, v=k^, and w=i^: (a×k^)×i^=(a⋅i^)k^−(k^⋅i^)a Since k^⋅i^=0, this simplifies to: (a×k^)×i^=(a⋅i^)k^ The dot product a⋅i^=a1. So, (a×k^)×i^=a1k^. The magnitude squared is ∣a1k^∣2=a12∣k^∣2=a12(1)2=a12. For a=i^+j^−2k^, a1=1, so the third term is 12=1.
Summation The total value is the sum of these three terms: Value = ∣(a×i^)×j^∣2+∣(a×j^)×i^∣2+∣(a×k^)×i^∣2 Value = a22+a12+a12 Substituting the values a1=1 and a2=1: Value = 12+12+12=1+1+1=3.
Alternatively, we can compute the cross products directly: a=i^+j^−2k^
-
a×i^=(i^+j^−2k^)×i^=(j^×i^)−2(k^×i^)=−k^−2j^. (a×i^)×j^=(−2j^−k^)×j^=−2(j^×j^)−(k^×j^)=0−(−i^)=i^. ∣(a×i^)×j^∣2=∣i^∣2=1.
-
a×j^=(i^+j^−2k^)×j^=(i^×j^)−2(k^×j^)=k^−2(−i^)=2i^+k^. (a×j^)×i^=(2i^+k^)×i^=2(i^×i^)+(k^×i^)=0+j^=j^. ∣(a×j^)×i^∣2=∣j^∣2=1.
-
a×k^=(i^+j^−2k^)×k^=(i^×k^)+(j^×k^)=−j^+i^. (a×k^)×i^=(i^−j^)×i^=(i^×i^)−(j^×i^)=0−(−k^)=k^. ∣(a×k^)×i^∣2=∣k^∣2=1.
Summing the magnitudes squared: 1+1+1=3.
The final answer is 3.
