Question

Correct option represents

• A. $x \in (3, 5] \cup [9, 11)$
• B. $x \in (3, 5] \cup [9, 11) - \{4\}$
• C. $x \in (3, 4) \cup (4, 5) \cup [3, 11)$
• D. $x \in (3, 4) \cup (4, 5] \cup (9, 11)$

Answer 1

Answer: (B)

(B)

Answer 2

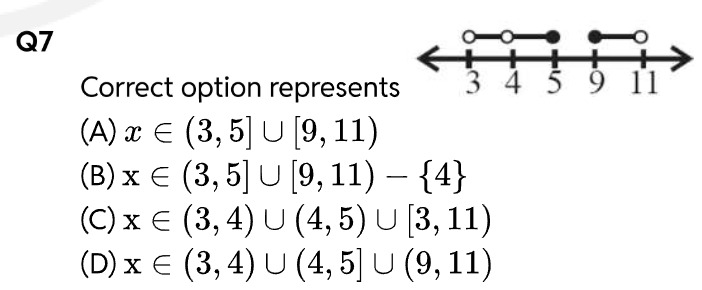
The number line shows a set of real numbers. Let's analyze the intervals shown. The first part of the set is represented by the thickened line segment between 3 and 5, with an open circle at 3, an open circle at 4, and a closed circle at 5.

An open circle at an endpoint means the endpoint is not included in the interval. A closed circle means the endpoint is included. The thickened line segment between two points indicates that all numbers between these points are included in the set, subject to the inclusion/exclusion of the endpoints and any intermediate points marked with open circles.

So, the first part represents the numbers $x$ such that $3 < x \le 5$, but with the number 4 excluded. This can be written as the interval $(3, 5]$ with the point 4 removed, i.e., $(3, 5] \setminus \{4\}$. The set $(3, 5] \setminus \{4\}$ can be expressed as the union of two disjoint intervals: $(3, 4)$ and $(4, 5]$.

$(3, 4) = \{x \in \mathbb{R} \mid 3 < x < 4\}$.

$(4, 5] = \{x \in \mathbb{R} \mid 4 < x \le 5\}$.

So, the first part of the set is $(3, 4) \cup (4, 5]$.

The second part of the set is represented by the thickened line segment between 9 and 11, with a closed circle at 9 and an open circle at 11. This represents the interval from 9 to 11, including 9 but excluding 11. This can be written as the interval $[9, 11)$.

$[9, 11) = \{x \in \mathbb{R} \mid 9 \le x < 11\}$.

The total set represented on the number line is the union of these two parts.

Set = $(3, 4) \cup (4, 5] \cup [9, 11)$.

Comparing with the given options:

(A) $x \in (3, 5] \cup [9, 11)$. This includes 4 in the interval $(3, 5]$.

(B) $x \in (3, 5] \cup [9, 11) - \{4\}$. This means $((3, 5] \cup [9, 11)) \setminus \{4\}$.

$((3, 5] \cup [9, 11)) \setminus \{4\} = ((3, 5] \setminus \{4\}) \cup ([9, 11) \setminus \{4\})$.

$(3, 5] \setminus \{4\} = (3, 4) \cup (4, 5]$.

Since $4 \notin [9, 11)$, $[9, 11) \setminus \{4\} = [9, 11)$.

So, option (B) represents $(3, 4) \cup (4, 5] \cup [9, 11)$. This matches our derived set.

(C) $x \in (3, 4) \cup (4, 5) \cup [3, 11)$. This is $(3, 5) \setminus \{4\} \cup [3, 11) = [3, 11)$.

(D) $x \in (3, 4) \cup (4, 5] \cup (9, 11)$. This is $(3, 5] \setminus \{4\} \cup (9, 11)$. This excludes 9.

Therefore, the correct option is (B).