Solveeit Logo
Login

Question

Question: Factorise the following expression $(x + y + z)^3 - x^3 - y^3 - z^3$....

Factorise the following expression

(x+y+z)3−x3−y3−z3(x + y + z)^3 - x^3 - y^3 - z^3.

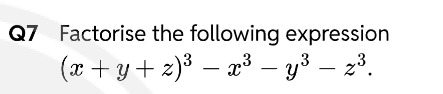
Answer

3(x+y)(y+z)(z+x)

Explanation

Solution

The expression is (x+y+z)3−x3−y3−z3(x+y+z)^3 - x^3 - y^3 - z^3.

Using the identity (a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)(a+b+c)^3 = a^3 + b^3 + c^3 + 3(a+b)(b+c)(c+a), with a=x,b=y,c=za=x, b=y, c=z, we get (x+y+z)3=x3+y3+z3+3(x+y)(y+z)(z+x)(x+y+z)^3 = x^3 + y^3 + z^3 + 3(x+y)(y+z)(z+x).

Rearranging this identity gives (x+y+z)3−x3−y3−z3=3(x+y)(y+z)(z+x)(x+y+z)^3 - x^3 - y^3 - z^3 = 3(x+y)(y+z)(z+x).

Alternatively, by applying the factor theorem, we find that (x+y)(x+y), (y+z)(y+z), and (z+x)(z+x) are factors. Since the expression is a homogeneous polynomial of degree 3, the factorisation must be k(x+y)(y+z)(z+x)k(x+y)(y+z)(z+x) for some constant kk. Comparing the coefficient of the xyzxyz term on both sides, we find k=3k=3.