Solveeit Logo
Login

Question

Question: Capacitor in circuit (i) is charged to a potential V while the one in circuit (ii) is uncharged. The...

Capacitor in circuit (i) is charged to a potential V while the one in circuit (ii) is uncharged. The switches S1S_1 and S2S_2 are closed at t = 0. The value of t at which the charge on the capacitor is circuit (ii) becomes twice the charge on the capacitor of circuit (i) is

A

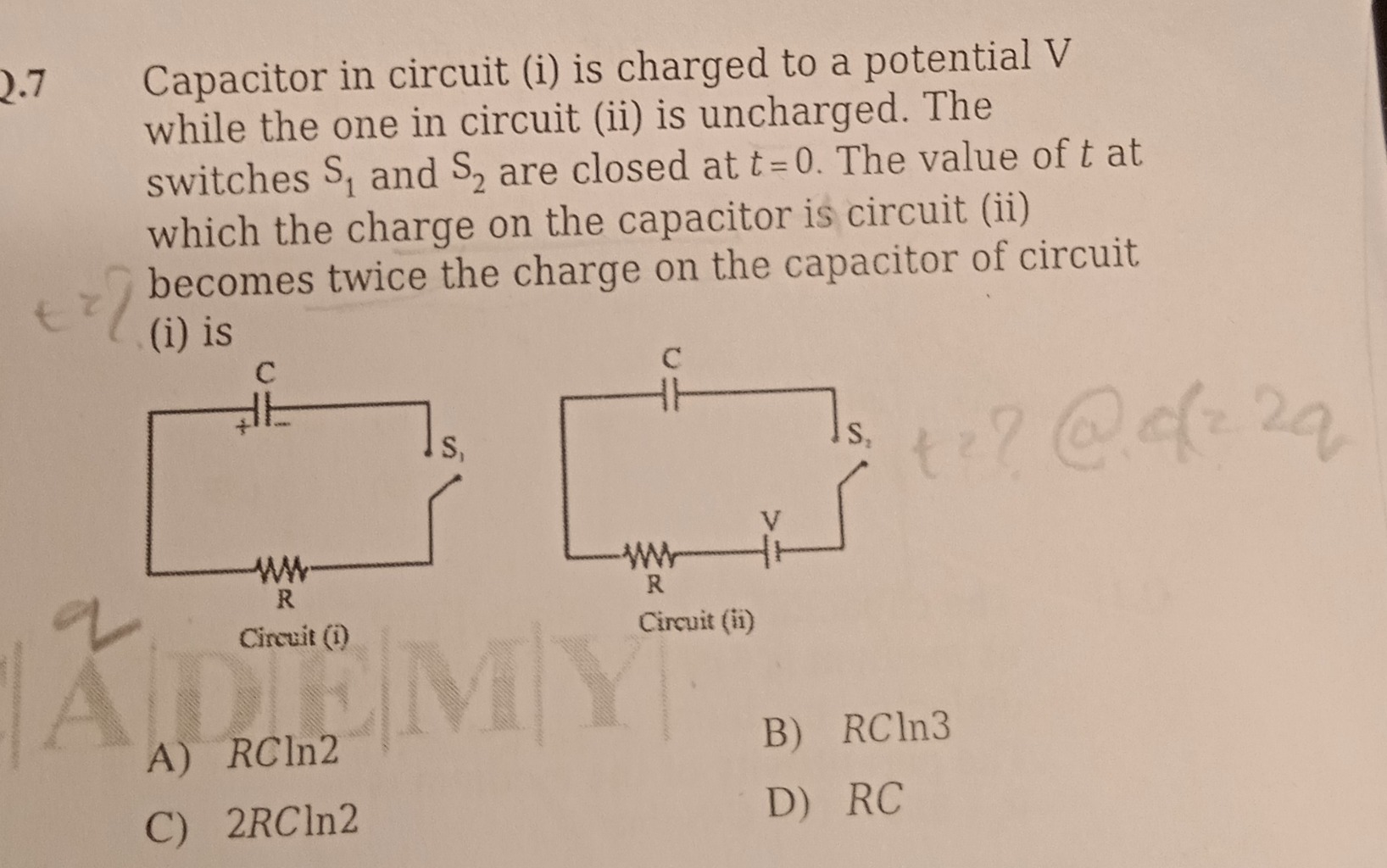
RCln2

B

RCln3

C

2RCln2

D

RC

Answer

RCln3

Explanation

Solution

The problem involves two RC circuits: one with a discharging capacitor and another with a charging capacitor. We need to find the time 't' when the charge on the capacitor in circuit (ii) becomes twice the charge on the capacitor in circuit (i).

1. Analyze Circuit (i) - Discharging Capacitor:

  • Initial charge on the capacitor at t=0 is Q0=CVQ_0 = CV, where C is the capacitance and V is the initial potential.
  • When the switch S1S_1 is closed, the capacitor discharges through the resistor R.
  • The charge on the capacitor at any time 't' during discharge is given by the formula: Q1(t)=Q0e−t/RCQ_1(t) = Q_0 e^{-t/RC} Substituting Q0=CVQ_0 = CV: Q1(t)=CVe−t/RCQ_1(t) = CV e^{-t/RC}

2. Analyze Circuit (ii) - Charging Capacitor:

  • Initial charge on the capacitor at t=0 is 0 (uncharged).
  • When the switch S2S_2 is closed, the capacitor charges through the resistor R due to the voltage source V.
  • The maximum charge the capacitor can store is Qmax=CVQ_{max} = CV.
  • The charge on the capacitor at any time 't' during charging is given by the formula: Q2(t)=Qmax(1−e−t/RC)Q_2(t) = Q_{max} (1 - e^{-t/RC}) Substituting Qmax=CVQ_{max} = CV: Q2(t)=CV(1−e−t/RC)Q_2(t) = CV (1 - e^{-t/RC})

3. Apply the given condition:

The problem states that the charge on the capacitor in circuit (ii) becomes twice the charge on the capacitor of circuit (i) at time 't'. So, Q2(t)=2Q1(t)Q_2(t) = 2 Q_1(t)

Substitute the expressions for Q1(t)Q_1(t) and Q2(t)Q_2(t): CV(1−e−t/RC)=2(CVe−t/RC)CV (1 - e^{-t/RC}) = 2 (CV e^{-t/RC})

4. Solve for 't':

Cancel out the common term CVCV from both sides (since C and V are non-zero): 1−e−t/RC=2e−t/RC1 - e^{-t/RC} = 2 e^{-t/RC}

Rearrange the terms to isolate the exponential term: 1=2e−t/RC+e−t/RC1 = 2 e^{-t/RC} + e^{-t/RC} 1=3e−t/RC1 = 3 e^{-t/RC}

Now, divide by 3: e−t/RC=13e^{-t/RC} = \frac{1}{3}

To solve for 't', take the natural logarithm (ln) of both sides: ln⁡(e−t/RC)=ln⁡(13)\ln(e^{-t/RC}) = \ln(\frac{1}{3})

Using the logarithm property ln⁡(ex)=x\ln(e^x) = x and ln⁡(a/b)=ln⁡(a)−ln⁡(b)\ln(a/b) = \ln(a) - \ln(b): −t/RC=ln⁡(1)−ln⁡(3)-t/RC = \ln(1) - \ln(3)

Since ln⁡(1)=0\ln(1) = 0: −t/RC=0−ln⁡(3)-t/RC = 0 - \ln(3) −t/RC=−ln⁡(3)-t/RC = -\ln(3)

Multiply both sides by -1: t/RC=ln⁡(3)t/RC = \ln(3)

Finally, solve for 't': t=RCln⁡(3)t = RC \ln(3)