Question
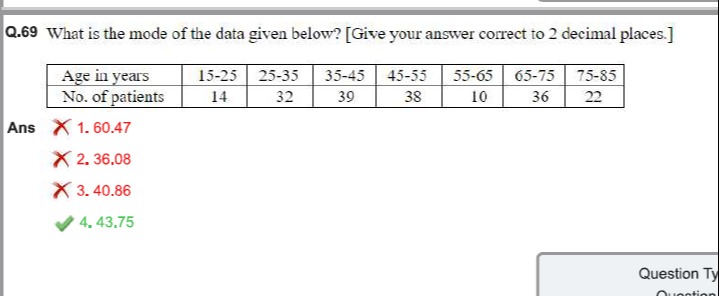
Question: What is the mode of the data given below? [Give your answer correct to 2 decimal places.] | Age in ...
What is the mode of the data given below? [Give your answer correct to 2 decimal places.]
| Age in years | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 |
|---|---|---|---|---|---|---|---|
| No. of patients | 14 | 32 | 39 | 38 | 10 | 36 | 22 |
A
60.47
B
36,08
C
40.86
D
43,75
Answer
43.75
Explanation
Solution
To find the mode of the given grouped data, we use the formula:
Mode = l+(2f1−f0−f2f1−f0)×h
Where:
- l = lower limit of the modal class
- h = size of the class interval
- f1 = frequency of the modal class
- f0 = frequency of the class preceding the modal class
- f2 = frequency of the class succeeding the modal class
Step 1: Identify the modal class.
The modal class is the class interval with the highest frequency. From the given data:
| Age in years | No. of patients (Frequency) |
|---|---|
| 15-25 | 14 |
| 25-35 | 32 |
| 35-45 | 39 |
| 45-55 | 38 |
| 55-65 | 10 |
| 65-75 | 36 |
| 75-85 | 22 |
The highest frequency is 39, which corresponds to the class interval 35-45. Therefore, the modal class is 35-45.
Step 2: Extract the values for the formula.
- Lower limit of the modal class (l) = 35
- Class size (h) = Upper limit - Lower limit = 45 - 35 = 10
- Frequency of the modal class (f1) = 39
- Frequency of the class preceding the modal class (f0) = 32 (frequency of 25-35)
- Frequency of the class succeeding the modal class (f2) = 38 (frequency of 45-55)
Step 3: Substitute the values into the mode formula and calculate.
Mode = 35+(2(39)−32−3839−32)×10
Mode = 35+(78−707)×10
Mode = 35+(87)×10
Mode = 35+870
Mode = 35+8.75
Mode = 43.75
The mode of the data is 43.75.
