Question

Let $$ be a sequence such that $a_1+a_2+...+a_n = \frac{n^2+3n}{(n+1)(n+2)}$. If $28\sum_{k=1}^{10}\frac{1}{a_k}=p_1p_2p_3...p_m$, where $p_1,p_2,...p_m$ are the first $m$ prime numbers, then $m$ is equal to

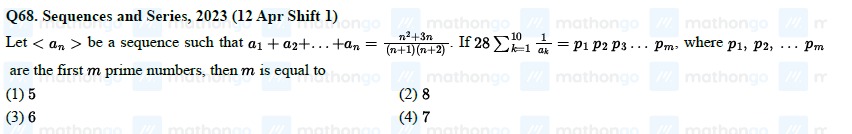
• A. 5
• B. 8
• C. 6
• D. 7

Answer 1

Answer: (C)

6

Answer 2

We are given that the partial sum

$$S_n = a_1 + a_2 + \cdots + a_n = \frac{n^2+3n}{(n+1)(n+2)}.$$

Then the $n^\text{th}$ term is:

$$a_n = S_n - S_{n-1}.$$

First, write:

$$S_n = \frac{n(n+3)}{(n+1)(n+2)}, \quad S_{n-1} = \frac{(n-1)^2+3(n-1)}{n(n+1)} = \frac{n^2+n-2}{n(n+1)}.$$

Thus,

$$a_n = \frac{n(n+3)}{(n+1)(n+2)} - \frac{n^2+n-2}{n(n+1)}.$$

Writing over a common denominator $n(n+1)(n+2)$:

$$a_n = \frac{n^2(n+3) - (n+2)(n^2+n-2)}{n(n+1)(n+2)}.$$

Expanding:

$$n^2(n+3)= n^3+3n^2,$$ $$(n+2)(n^2+n-2)= n^3+3n^2-4.$$

So,

$$a_n = \frac{(n^3+3n^2) - (n^3+3n^2-4)}{n(n+1)(n+2)} = \frac{4}{n(n+1)(n+2)}.$$

Now, compute

$$\sum_{k=1}^{10}\frac{1}{a_k} = \sum_{k=1}^{10} \frac{k(k+1)(k+2)}{4}.$$

That is,

$$\sum_{k=1}^{10}\frac{1}{a_k} = \frac{1}{4}\sum_{k=1}^{10} k(k+1)(k+2).$$

Note that

$$k(k+1)(k+2)= k^3+3k^2+2k.$$

Thus,

$$\sum_{k=1}^{10} \bigl(k^3+3k^2+2k\bigr)= \sum_{k=1}^{10} k^3 + 3\sum_{k=1}^{10} k^2 + 2\sum_{k=1}^{10} k.$$

Using standard formulas:

$$\sum_{k=1}^{10} k = 55,\quad \sum_{k=1}^{10} k^2 = 385,\quad \sum_{k=1}^{10} k^3 = (55)^2=3025.$$

Hence,

$$3025+ 3(385) + 2(55)= 3025+1155+110=4290.$$

Thus,

$$\sum_{k=1}^{10}\frac{1}{a_k} = \frac{4290}{4} = \frac{4290}{4}.$$

Then, the given expression becomes:

$$28\sum_{k=1}^{10}\frac{1}{a_k} = 28 \times \frac{4290}{4} = 7 \times 4290 = 30030.$$

Notice that

$$30030 = 2 \times 3 \times 5 \times 7 \times 11 \times 13,$$

which is the product of the first 6 primes. Therefore, $m=6$.