Question

Let adj (1) = $\begin{bmatrix} 2 & 1 & 3 \\ 3 & 1 & 2 \\ 2 & 2 & -1 \end{bmatrix}$

then the value of det (adj (adj 2A)) is

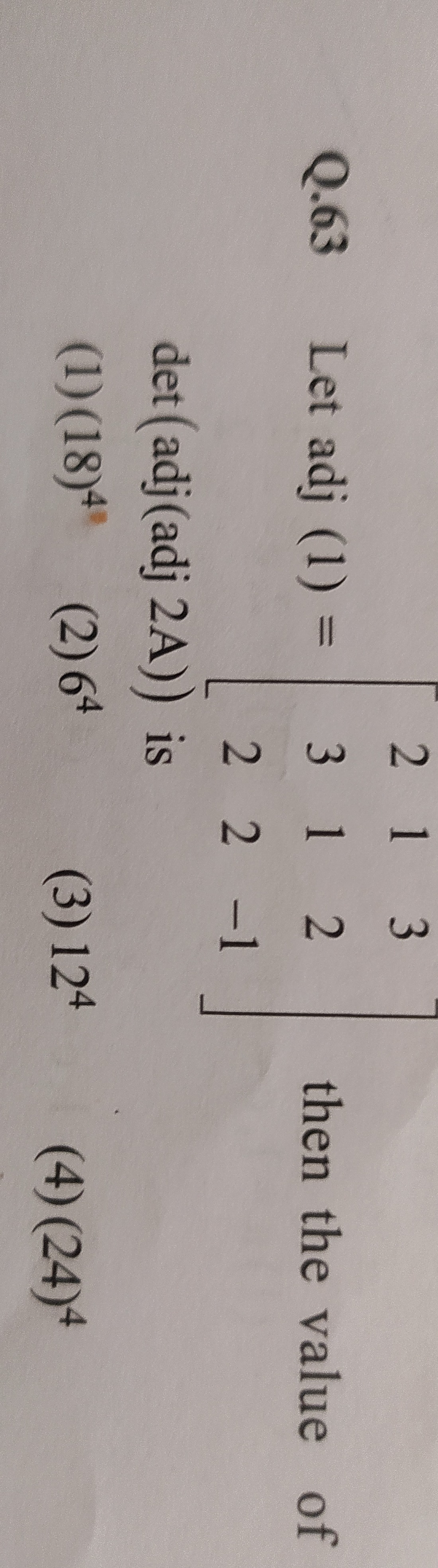
• A. (1)(18)4
• B. 64
• C. 124
• D. (24)4

Answer 1

Answer: (D)

(24)^4

Answer 2

Let A be a square matrix of order n. We are given adj(A) as a 3x3 matrix, so the order of matrix A is n=3.

Let $B = \text{adj}(A) = \begin{bmatrix} 2 & 1 & 3 \\ 3 & 1 & 2 \\ 2 & 2 & -1 \end{bmatrix}$. The order of B is 3x3, so n=3.

First, we calculate the determinant of adj(A). $\det(\text{adj}(A)) = \det\begin{bmatrix} 2 & 1 & 3 \\ 3 & 1 & 2 \\ 2 & 2 & -1 \end{bmatrix}$ $= 2(1(-1) - 2(2)) - 1(3(-1) - 2(2)) + 3(3(2) - 1(2))$ $= 2(-1 - 4) - 1(-3 - 4) + 3(6 - 2)$ $= 2(-5) - 1(-7) + 3(4)$ $= -10 + 7 + 12 = 9$.

For a square matrix A of order n, we have the property $\det(\text{adj}(A)) = (\det(A))^{n-1}$. In this case, n=3, so $\det(\text{adj}(A)) = (\det(A))^{3-1} = (\det(A))^2$. We found $\det(\text{adj}(A)) = 9$. So, $(\det(A))^2 = 9$.

We need to find the value of $\det(\text{adj}(\text{adj}(2A)))$. For a square matrix X of order n, we have the property $\det(\text{adj}(X)) = (\det(X))^{n-1}$. Applying this property twice, let Y = adj(X). Then $\det(\text{adj}(Y)) = (\det(Y))^{n-1}$. Substituting Y = adj(X), we get $\det(\text{adj}(\text{adj}(X))) = (\det(\text{adj}(X)))^{n-1}$. Using $\det(\text{adj}(X)) = (\det(X))^{n-1}$, we get $\det(\text{adj}(\text{adj}(X))) = ((\det(X))^{n-1})^{n-1} = (\det(X))^{(n-1)^2}$.

In our problem, X = 2A and n=3. So, $\det(\text{adj}(\text{adj}(2A))) = (\det(2A))^{(3-1)^2} = (\det(2A))^{2^2} = (\det(2A))^4$.

For a scalar k and a square matrix A of order n, we have the property $\det(kA) = k^n \det(A)$. In our case, k=2 and A is of order n=3. So, $\det(2A) = 2^3 \det(A) = 8 \det(A)$.

Substitute this into the expression for $\det(\text{adj}(\text{adj}(2A)))$: $\det(\text{adj}(\text{adj}(2A))) = (8 \det(A))^4 = 8^4 (\det(A))^4$.

We know that $(\det(A))^2 = 9$. So, $(\det(A))^4 = ((\det(A))^2)^2 = 9^2 = 81$.

Substitute this value back into the expression: $\det(\text{adj}(\text{adj}(2A))) = 8^4 \times 81$. $8^4 = (2^3)^4 = 2^{12} = 4096$. So, $\det(\text{adj}(\text{adj}(2A))) = 4096 \times 81$.

Now, we calculate the product: $4096 \times 81 = 4096 \times (80 + 1) = 4096 \times 80 + 4096 \times 1$ $= 327680 + 4096 = 331776$.

Now let's check the given options, assuming the format (x)y means $x^y$. (1) $(18)^4 = (2 \times 3^2)^4 = 2^4 \times 3^8 = 16 \times 6561 = 104976$. (2) $64$. (3) $124$. (4) $(24)^4 = (2^3 \times 3)^4 = (2^3)^4 \times 3^4 = 2^{12} \times 3^4 = 4096 \times 81 = 331776$.

The calculated value matches option (4).