Question
Question: The equation of the stationary wave is $y = 2A \sin(\frac{2 \pi ct}{\lambda}) \cos(\frac{2 \pi x}{\...
The equation of the stationary wave is
y=2Asin(λ2πct)cos(λ2πx)
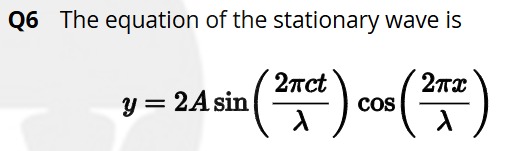
Answer
The maximum amplitude is 2A.
Explanation
Solution
The given equation represents a stationary wave. The amplitude of the wave is not constant but varies with position x. The amplitude at position x is given by A(x)=∣2Acos(λ2πx)∣. The maximum amplitude is 2A, which occurs at antinodes. Therefore, the maximum displacement amplitude of the stationary wave is $2A.
