Question
Question: Let $z$ be a complex number satisfying $\left(z+\frac{1}{z}\right)$ $\left(z+\frac{1}{z}+1\right)=1...
Let z be a complex number satisfying (z+z1)
(z+z1+1)=1. Then the value of
(3z100+z1002+1)(z100+z1002+3) equals to
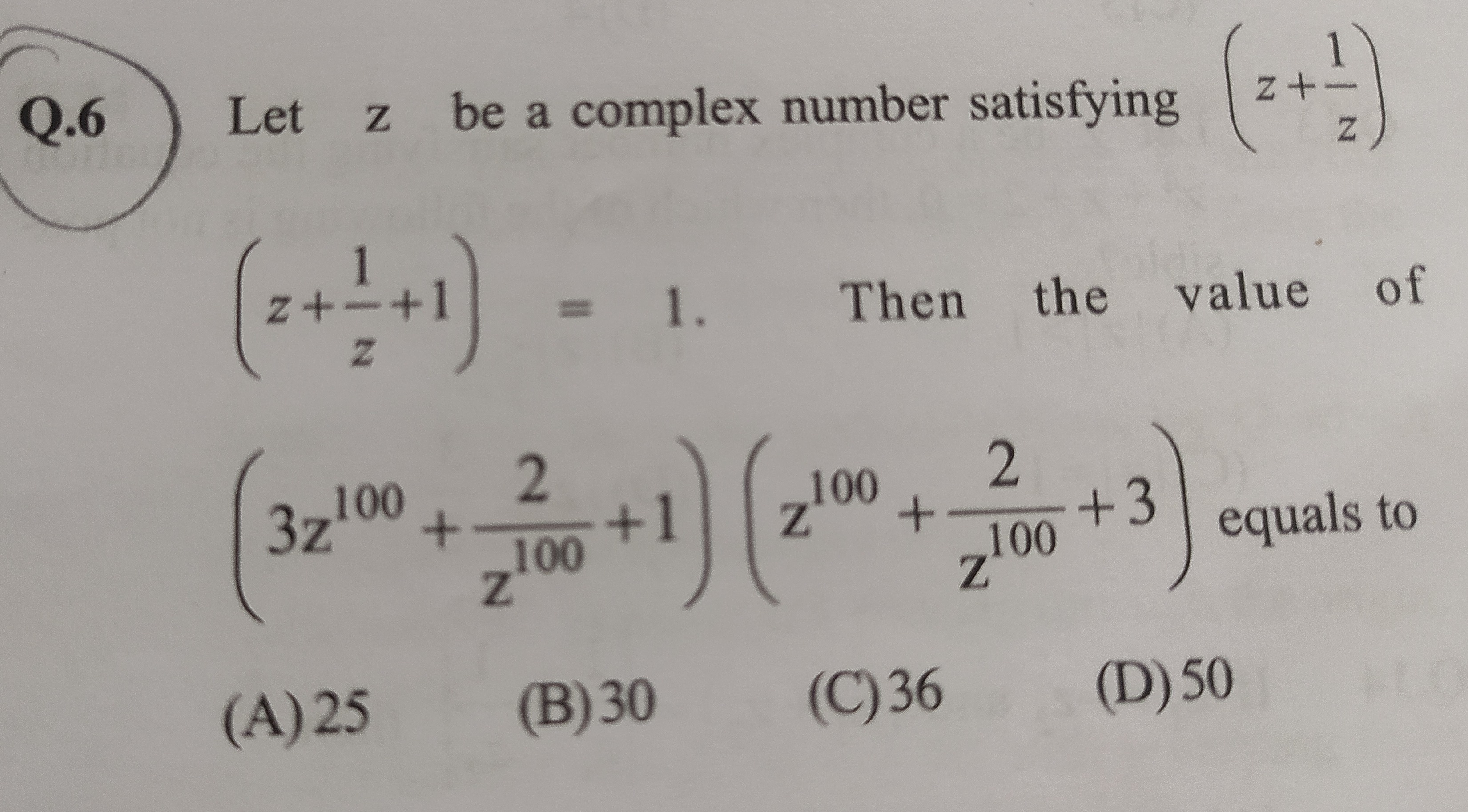
25
30
36
50
36
Solution
We first note that since z lies on the unit circle (as will be clear later), we can write
z=eiθ so that z+z1=eiθ+e−iθ=2cosθ.
The given condition is (z+z1)⋅(z+z1+1)=1.
Substitute t=z+z1=2cosθ. Then the condition becomes
t(t+1)=1⟹t2+t−1=0.
One could solve for t, but it is more convenient to return to the trigonometric form: 2cosθ(2cosθ+1)=1⟹4cos2θ+2cosθ−1=0.
Solving this quadratic in cosθ, we get cosθ=4−1±5.
Notice that cosθ=45−1≈0.309 corresponds to θ=72∘ (or equivalently 52π radians)
and cosθ=4−5−1 gives another valid angle (144∘). In either case, since ∣z∣=1, when we raise z to a high power the exponent will effectively be reduced modulo 360∘.
Consider z100=ei100θ. For θ=72∘, we have:
100θ=100×72∘=7200∘. Since 7200∘/360∘=20 exactly, it follows that
z100=ei7200∘=1.
Similarly, for the other value of θ, z100 will also be 1 because 100θ will be an integral multiple of 360∘.
Now the given expression is (3z100+z1002+1)⋅(z100+z1002+3).
Since z100=1 and z1001=1, the expression reduces to
(3⋅1+2⋅1+1)⋅(1+2⋅1+3)=(3+2+1)(1+2+3)=6⋅6=36.
Thus, the value is 36.
